题目内容
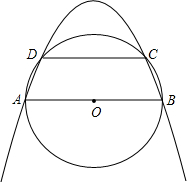 已知:如图,AB是⊙O的直径,CD是⊙O的一条非直径的弦,且AB∥CD,连接AD和BC,
已知:如图,AB是⊙O的直径,CD是⊙O的一条非直径的弦,且AB∥CD,连接AD和BC,(1)AD和BC相等吗?为什么?
(2)如果AB=2AD=4,且A、B、C、D四点在同一抛物线上,请在图中建立适当的直角坐标系,求出该抛物线的解析式.
(3)在(2)中所求抛物线上是否存在点P,使得S△PAB=
| 1 | 2 |
分析:(1)根据平行弦所夹的弧相等,在同圆或等圆中,等弧所对的弦相等解答;
(2)以圆心O为坐标原点,AB所在的直线为x轴,AB的垂直平分线为y轴建立平面直角坐标系,先求出点A、B的坐标,再连接OD,过点D作DE⊥AO于点E,可以证明△AOD是等边三角形,然后求出OE、DE的长度,从而得到点D的坐标,再利用待定系数法求二次函数解析式解答;
(3)根据对称性求出CD的长度,然后求出四边形ABCD的面积,然后求出点P到x轴的距离,再分点P在x轴上方与下方两种情况得到点P的纵坐标,代入抛物线解析式计算求出点P的横坐标,即可得解.
(2)以圆心O为坐标原点,AB所在的直线为x轴,AB的垂直平分线为y轴建立平面直角坐标系,先求出点A、B的坐标,再连接OD,过点D作DE⊥AO于点E,可以证明△AOD是等边三角形,然后求出OE、DE的长度,从而得到点D的坐标,再利用待定系数法求二次函数解析式解答;
(3)根据对称性求出CD的长度,然后求出四边形ABCD的面积,然后求出点P到x轴的距离,再分点P在x轴上方与下方两种情况得到点P的纵坐标,代入抛物线解析式计算求出点P的横坐标,即可得解.
解答:解:(1)AD=BC.
理由如下:∵AB∥CD,
∴
=
,
∴AD=BC;
(2)如图,建立平面直角坐标系,∵AB=2AD=4,
∴AO=BO=2,
∴点A、B的坐标分别为A(-2,0),B(2,0),
连接OD,过点D作DE⊥AO于点E,
则OD=AO=2,
∴△AOD是等边三角形,
OE=
AO=
×2=1,
DE=
=
=
,
∴点D的坐标为(-1,
),
设过A、B、C、D四点的抛物线解析式为y=ax2+bx+c,
则
,
解得
,
所以,该抛物线的解析式为y=-
x2+
;
(3)存在.理由如下:
由对称性可得CD=2OE=2×1=2,
∴S四边形ABCD=
×(2+4)×
=3
,
设点P到AB的距离为h,∵S△PAB=
S四边形ABCD,
∴
×4•h=
×3
,
解得h=
,
①当点P在x轴上方时,点P的纵坐标为
,
所以,-
x2+
=
,
解得x=±
,
此时,点P的坐标为(-
,
)或(
,
),
②当点P在x轴下方时,点P的纵坐标为-
,
所以,-
x2+
=-
,
解得x=±
,
此时,点P的坐标为(-
,-
)或(
,-
),
综上所述,抛物线上存在点P(-
,
)或(
,
)或(-
,-
)或(
,-
),使得S△PAB=
S四边形ABCD.
理由如下:∵AB∥CD,
∴
 |
| AD |
 |
| BC |
∴AD=BC;
(2)如图,建立平面直角坐标系,∵AB=2AD=4,
∴AO=BO=2,
∴点A、B的坐标分别为A(-2,0),B(2,0),
连接OD,过点D作DE⊥AO于点E,

则OD=AO=2,
∴△AOD是等边三角形,
OE=
| 1 |
| 2 |
| 1 |
| 2 |
DE=
| OD2-OE2 |
| 22-12 |
| 3 |
∴点D的坐标为(-1,
| 3 |
设过A、B、C、D四点的抛物线解析式为y=ax2+bx+c,
则
|
解得
|
所以,该抛物线的解析式为y=-
| ||
| 3 |
4
| ||
| 3 |
(3)存在.理由如下:
由对称性可得CD=2OE=2×1=2,
∴S四边形ABCD=
| 1 |
| 2 |
| 3 |
| 3 |
设点P到AB的距离为h,∵S△PAB=
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
解得h=
3
| ||
| 4 |
①当点P在x轴上方时,点P的纵坐标为
3
| ||
| 4 |
所以,-
| ||
| 3 |
4
| ||
| 3 |
3
| ||
| 4 |
解得x=±
| ||
| 2 |
此时,点P的坐标为(-
| ||
| 2 |
3
| ||
| 4 |
| ||
| 2 |
3
| ||
| 4 |
②当点P在x轴下方时,点P的纵坐标为-
3
| ||
| 4 |
所以,-
| ||
| 3 |
4
| ||
| 3 |
3
| ||
| 4 |
解得x=±
| 5 |
| 2 |
此时,点P的坐标为(-
| 5 |
| 2 |
3
| ||
| 4 |
| 5 |
| 2 |
3
| ||
| 4 |
综上所述,抛物线上存在点P(-
| ||
| 2 |
3
| ||
| 4 |
| ||
| 2 |
3
| ||
| 4 |
| 5 |
| 2 |
3
| ||
| 4 |
| 5 |
| 2 |
3
| ||
| 4 |
| 1 |
| 2 |
点评:本题综合考查了二次函数的问题,主要利用了平行弦所夹的弧相等,等弧所对的弦相等,等腰梯形的性质,等边三角形的判定与性质,待定系数法求二次函数解析式,二次函数图象上的点的特征,(3)注意要分点P在x轴上方与下方两种情况讨论.

练习册系列答案
相关题目
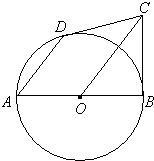 22、已知:如图,AB是⊙O的直径,BC是和⊙O相切于点B的切线,⊙O的弦AD平行于OC.
22、已知:如图,AB是⊙O的直径,BC是和⊙O相切于点B的切线,⊙O的弦AD平行于OC.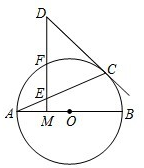 (2013•门头沟区一模)已知:如图,AB是⊙O的直径,AC是⊙O的弦,M为AB上一点,过点M作DM⊥AB,交弦AC于点E,交⊙O于点F,且DC=DE.
(2013•门头沟区一模)已知:如图,AB是⊙O的直径,AC是⊙O的弦,M为AB上一点,过点M作DM⊥AB,交弦AC于点E,交⊙O于点F,且DC=DE.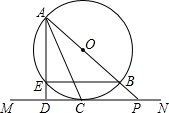 (1997•昆明)已知:如图,AB是⊙O的直径,直线MN切⊙O于点C,AD⊥MN于D,AD交⊙O于E,AB的延长线交MN于点P.求证:AC2=AE•AP.
(1997•昆明)已知:如图,AB是⊙O的直径,直线MN切⊙O于点C,AD⊥MN于D,AD交⊙O于E,AB的延长线交MN于点P.求证:AC2=AE•AP.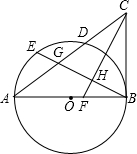 (2012•平谷区二模)已知,如图,AB是⊙O的直径,点E是
(2012•平谷区二模)已知,如图,AB是⊙O的直径,点E是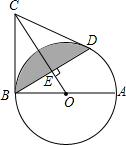 已知:如图,AB是⊙O的直径,BC为⊙O的切线,过点B的弦BD⊥OC交⊙O于点D,垂足为E.
已知:如图,AB是⊙O的直径,BC为⊙O的切线,过点B的弦BD⊥OC交⊙O于点D,垂足为E.