题目内容
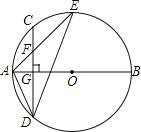
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足![]() =
=![]() ,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.
,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.
(1)求证:△ADF∽△AED;
(2)求FG的长;
(3)求证:tan∠E=![]() .
.

【答案】①证明见解析;
②2;
③证明见解析.
【解析】试题分析:(1)由垂径定理可得弧AC=弧AD,根据等弧所对的圆周角相等,可得∠ADF=∠AED,,根据两角对应相等的两个三角形相似的判定定理,即可证得△ADF∽△AED;
(2)根据![]() =
=![]() ,CF=2,可得FD=6,故可得CD的长,根据垂径定理即可求得CG的长,再根据CG-CF即可得FG的长。
,CF=2,可得FD=6,故可得CD的长,根据垂径定理即可求得CG的长,再根据CG-CF即可得FG的长。
(3)在Rt△AGF中由勾股定理求得AG的长,根据垂径定理和同弧所对的圆周角相等的性质,可知∠E=∠ADF,再根据三角函数定义即可证得tanE的值.
解:①∵AB是⊙O的直径,弦CD⊥AB,
∴DG=CG,
∴弧AD=弧AC,∠ADF=∠AED,
∵∠FAD=∠DAE(公共角),
∴△ADF∽△AED;
②∵![]() =
=![]() ,CF=2,
,CF=2,
∴FD=6,
∴CD=DF+CF=8,
∴CG=DG=4,
∴FG=CG﹣CF=2;
③∵AF=3,FG=2,∴AG=![]() ,
,
tan∠E=![]() .
.

练习册系列答案
相关题目







