题目内容
【题目】已知：AB为⊙O的直径，延长AB到点P，过点P作圆O的切线，切点为C，连接AC，且AC=CP.
（1）求∠P的度数；
（2）若点D是弧AB的中点，连接CD交AB于点E，且DE·DC=20，求⊙O的面积.（π取3.14）
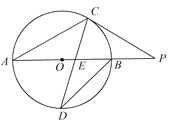
【答案】（1）∠P=30°；（2）31.4.
【解析】
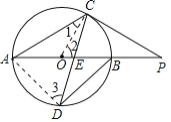
（1）连接OC，根据圆的切线的性质可得∠2＋∠P＝90°，根据等腰三角形的性质可得∠P＝∠CAO，再根据三角形外角的性质可得∠2＝2∠P，进而可求出∠P的度数；（2）连接AD，根据等弧对等角得到∠ACD＝∠DAE，故△ACD∽△DAE，然后根据相似比求出AD的长，再根据“直径所对的角是90°”以及AD＝BD得到Rt△ADB是等腰直角三角形，根据等腰直角三角形的性质求出OA的长，进而可求出⊙O的面积.
（1）连接
，
为
的切线，
，即
，
，
，
，
，
又
是
的一个外角，
，
，
；
（2）连接
，
为
的中点，
，
，
，即
，
，
，
，
，
是的直径，
为等腰直角三角形，
，
，
．
【题目】自2016年国庆后，许多高校均投放了使用手机就可随用的共享单车．某运营商为提高其经营的A品牌共享单车的市场占有率，准备对收费作如下调整：一天中，同一个人第一次使用的车费按0.5元收取，每增加一次，当次车费就比上次车费减少0.1元，第6次开始，当次用车免费．具体收费标准如下：
使用次数 | 0 | 1 | 2 | 3 | 4 | 5(含5次以上) |
累计车费 | 0 | 0.5 | 0.9 |
|
| 1.5 |
同时，就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿，得到如下数据：
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 5 | 15 | 10 | 30 | 25 | 15 |
（Ⅰ）写出
的值；
（Ⅱ）已知该校有5000名师生，且A品牌共享单车投放该校一天的费用为5800元．试估计：收费调整后，此运营商在该校投放A品牌共享单车能否获利? 说明理由．
【题目】光明中学全体学生1100人参加社会实践活动，从中随机抽取50人的社会实践活动成绩制成如图所示的条形统计图，结合图中所给信息解答下列问题：
（1）填写下表：
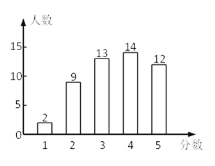
中位数 | 众数 | |
随机抽取的50人的社会实践活动成绩（单位：分） |
（2）估计光明中学全体学生社会实践活动成绩的总分．
