Question

【题目】如图，在正方形ABCD中，对角线AC、BD相交于点O，E、F分别在OD、OC上的动点，且DE=CF，连接DF、AE，AE的延长线交DF于点M，连接OM．

（1）求证：△ADE≌△DCF；

（2）求证：AM⊥DF；

（3）当CD=AF时，试判断△MOF的形状，并说明理由．

Answer 1

【答案】（1）证明见解析；（2）证明见解析.（3）△MOF是等腰三角形，理由见解析.

【解析】

（1）根据DE=CF和正方形的性质，证明△AED≌△DFC；

（2）由△AED≌△DFC得出∠EAD=∠FDC，然后利用等角代换可得出∠AMD=90°，得出了结论．

（2）利用等腰三角形三线合一得：DM=FM，再由直角三角形斜边中线可得结论．

（1）证明：∵四边形ABCD是正方形，

∴AD=DC，∠ADE=∠DCF=45°

在△AED和△DFC中，

，

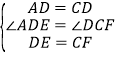∴△AED≌△DFC（SAS）；

（2）由①中△AED≌△DFC，

∴∠EAD=∠FDC，

∵∠ADM+∠FDC=90°，

∴∠ADM+∠EAD=90°，

∴∠AMD=90°，

∴AM⊥DF；

（3）△MOF是等腰三角形，

理由是：∵AD=CD，CD=AF

∴AD=AF

∵AM⊥DF，

∴DM=FM，

∵∠DOF=90°，

∴OM=DF=FM，

∴△MOF是等腰三角形．