题目内容
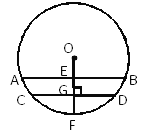
【题目】如图，圆柱形水管内原有积水的水平面宽CD=10cm，水深GF=1cm，若水面上升1cm（EG=1cm），则此时水面宽AB为多少？
【答案】AB=
【解析】试题分析：
试题解析：连接OA、OC．设 O的半径是R，则OG=R-1，OE=R-2．根据垂径定理，得CG=5．在直角三角形OCG中，根据勾股定理求得R的值，再进一步在直角三角形OAE中，根据勾股定理求得AE的长，从而再根据垂径定理即可求得AB的长．
试题解析：如图所示，
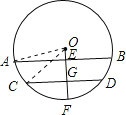
连接OA、OC.
设O的半径是R，则OG=R1，OE=R2.
∵OF⊥CD，
∴CG=
CD=5cm.
在直角三角形COG中，根据勾股定理，得
R2=52+(R1)2，
解，得R=13.
在直角三角形AOE中，根据勾股定理，得
AE=
=
=
=
cm.
根据垂径定理,得AB=2AE=
(cm).
则此时水面宽AB为
cm.
练习册系列答案
相关题目
【题目】为了解某班学生每天使用零花钱的情况，小红随机调查了15名同学，结果如下表：
每天使用零花钱 | 1 | 2 | 3 | 5 | 6 |
人 数 | 2 | 5 | 4 | 3 | 1 |
则这15名同学每天使用零花钱的众数和中位数分别是（ ）
A.3，3
B.2，3
C.2，2
D.3，5
