题目内容
【题目】如图，在平面直角坐标系xOy中，直线y＝kx＋b交x轴于点A，交y轴于点B，线段AB的中点E的坐标为(2，1)．
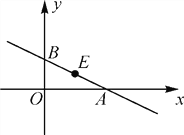
(1)求k，b的值；
(2)P为直线AB上一点，PC⊥x轴于点C，PD⊥y轴于点D，若四边形PCOD为正方形，求点P的坐标．
【答案】 (1)k＝－
，b＝2；(2)点P的坐标为(
，)或(－4，4)
【解析】【试题分析】（1）根据中点的坐标求出A、B的坐标，列出方程组求解即可；
（2）根据正方形的边长相等列出方程，求解即可.
【试题解析】
（1）因为线段AB的中点E的坐标为(2，1)．
所以A( 4，0 ),B( 0，2 )，将A、B两点代入y＝kx＋b，
得：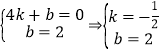
，所以k＝－，b＝2.
(2)根据正方形的边长，设P(a,a)或（a,-a）,得方程：
.
故点P的坐标为(，)或(－4，4).
练习册系列答案
相关题目
