Question

【题目】已知,在△ABC中,AC = BC.分别过A,B点作互相平行的直线AM和BN.过点C的直线分别交直线AM，BN于点D，E。

(1)如图1.若CD= CE .求∠ABE的大小:

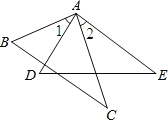
(2)如图2.∠ABC= ∠DEB= 60°.求证:AD+DC = BE.

Answer 1

【答案】（1）90°；（2）见详解

【解析】

（1）延长AC交BN于点F，依据条件得到∠FEC=∠ADC，证明△ADC≌△FEC，进而得到AC=FC, ∠DAC=∠EFC，依据等角替换与平角得出，即可得出∠ABE的大小；
（2）在EB上截取EH=EC，连CH，判定△DAC≌△HCB（AAS），即可得到AD=CH，DC=BH，再根据CH=CE=HE，即可得到BE=BH+HE=DC+AD．

解：：（1）如图1，延长AC交BN于点F，

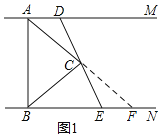
∵AM∥BN，
∴∠FEC=∠ADC
在△ADC和△FEC中，

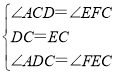
∴△ADC≌△FEC（ASA），

∴AC=FC，∠DAC=∠EFC
∵AC=BC
∴AC=BC=FC

∴∠CBE=∠CFE，∠DAC=∠CBE

∴∠DAB+∠ABE=180°，2∠ABC+2∠CBE=180°

∴∠ABC+∠CBE=90°

即∠ABE=90°；

（2）如图2，在EB上截取EH=EC，连CH，

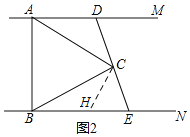
∵AC=BC，∠ABC=60°，
∴△ABC为等边三角形，
∵∠DEB=60°，
∴△CHE是等边三角形，
∴∠CHE=60°，∠HCE=60°，
∴∠BHC=120°，
∵AM∥BN，
∴∠ADC+∠BEC=180°，
∴∠ADC=120°，
∴∠DAC+∠DCA=60°，
又∵∠DCA+∠ACB+∠BCH+∠HCE=180°，
∴∠DCA+∠BCH=60°，
∴∠DAC=∠BCH，
在△DAC与△HCB中，

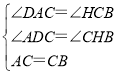
∴△DAC≌△HCB（AAS），
∴AD=CH，DC=BH，
又∵CH=CE=HE，
∴BE=BH+HE=DC+AD．