题目内容
【题目】如图,四边形ABCD中,∠A=∠C=90°,∠ABC=60°,AD=4,CD=10,则BD的长等于 . 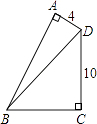
【答案】4 ![]()
【解析】解: 延长BA、CD交于E,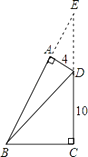
∵∠C=90°,∠ABC=60°,
∴∠E=180°﹣90°﹣60°=30°,
∴DE=2AD=8,
∴CE=10+8=18,
∵tan∠ABC= ![]() ,
,
∴tan60°= ![]() ,
,
BC=6 ![]() ,
,
在Rt△BCD中,由勾股定理得:BD= ![]() =
= ![]() =4
=4 ![]() .
.
所以答案是:4 ![]() .
.
【考点精析】通过灵活运用三角形的内角和外角和含30度角的直角三角形,掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半即可以解答此题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目