题目内容
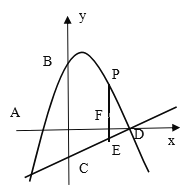
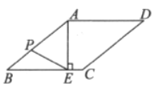
【题目】如图,在菱形![]() 中,点
中,点![]() 是
是![]() 上的点,
上的点,![]() ,若
,若![]() ,
,![]() ,
,![]() 是
是![]() 边上的一个动点,则线段
边上的一个动点,则线段![]() 最小时,
最小时,![]() 长为___________.
长为___________.
【答案】![]()
【解析】
设菱形ABCD的边长为x,则AB=BC=x,又EC=3,所以BE=x3,解直角△ABE即可求得x的值,即可求得BE、AE的值,根据AB、PE的值和△ABE的面积,即可求得PE的最小值,再根据勾股定理可得![]() 的长.
的长.
解:设菱形ABCD的边长为x,则AB=BC=x,又EC=3,所以BE=x3,
因为AE⊥BC于E,
所以在Rt△ABE中,![]() ,
,
∵![]() ,AE⊥BC
,AE⊥BC
设AE=3a,AB=5a,则BE=4a,
∴cosB=![]()
∴![]()
于是5x15=4x,
解得x=15,即AB=15.
所以易求BE=12,AE=9,
当EP⊥AB时,PE取得最小值.
故由三角形面积公式有:![]() ABPE=
ABPE=![]() BEAE,
BEAE,
求得PE的最小值为![]() .
.
在Rt△BPE中,BP=![]()
故答案为:![]() .
.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目