Question

【题目】已知点A（0，4），B（7，0），C（7，4），连接AC，BC得到矩形AOBC，点D的边AC上，将边OA沿OD折叠，点A的对应边为A'．若点A'到矩形较长两对边的距离之比为1：3，则点A'的坐标为 ．

Answer 1

【答案】

【解析】

试题分析：由点A（0，4），B（7，0），C（7，4），可得BC=OA=4，OB=AC=7，

分两种情况：

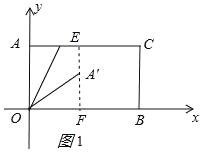
（1）当点A'在矩形AOBC的内部时，过A'作OB的垂线交OB于F，交AC于E，如图1所示：

①当A'E：A'F=1：3时，

∵A'E+A'F=BC=4，

∴A'E=1，A'F=3，

由折叠的性质得：OA'=OA=4，

在Rt△OA'F中，由勾股定理得：OF== ，

∴A'（，3）；

②当A'E：A'F=3：1时，同理得：A'（，1）；

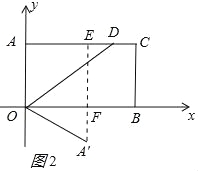
（2）当点A'在矩形AOBC的外部时，此时点A'在第四象限，过A'作OB的垂线交OB于F，交AC于E，如图2所示：∵A'F：A'E=1：3，则A'F：EF=1：2，

∴A'F=EF=BC=2，

由折叠的性质得：OA'=OA=4，

在Rt△OA'F中，由勾股定理得：OF==2，

∴A'（2，﹣2）；

故答案为：（，3）或（，1）或（2，﹣2）．