Question

如图，在正方形ABCD中，AD=8，点E是边CD上（不包括端点）的动点，AE的中垂线FG分别交AD，AE，BC于点F，H，K交AB的延长线于点G．
（1）设DE=m，

FH

HK

=t，用含m的代数式表示t；
（2）当t=

1

3

时，求BG的长．

Answer 1

分析：（1）过点H作MN∥CD交AD，BC于M，N，根据矩形的性质及平行线的性质可得到FH：HK=HM：HN，从而可用含m的代数式表示t；
（2）过点H作HT⊥AB于T，根据正方形的性质及平行线的性质可求得BG的长．

解答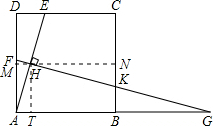：解：（1）过点H作MN∥CD交AD，BC于M，N，则四边形ABNM是矩形，
∴MN=AB=AD，
∵FG是AE的中垂线，
∴H为AE的中点，
∴MH=

1

2

DE=

1

2

m，HN=8-

1

2

m，
∵AM∥BC，
∴FH：HK=HM：HN=（

1

2

m）：（8-

1

2

m），
∴t=

m

16-m

．

（2）过点H作HT⊥AB于T，
当t=

1

3

时，

m

16-m

=

1

3

，解得m=4，即DE=4，
在Rt△ADE中，由勾股定理得，AE²=AD²+DE²=80，
∴AE=4

5

，
∴AH=

1

2

AE=2

5

，
∵AF∥HT∥BK，
∴AT：BT=FH：HK=t=

1

3

，
∵AB=8，
∴AT=2，BT=6．
在直角△AHG中，HT⊥AG，
∴△AHT∽△HGT，
∴TH：TG=AT：HT，
∴TG=HT²：AT．
在直角△AHT中，HT²=AH²-AT²=16，
∴HT=4，
∴TG=4²÷2=8，
∴BG=TG-BT=8-6=2．

点评：本题利用了中垂线的性质，正方形和矩形的性质，平行线分线段成比例，勾股定理，相似三角形的判定和性质求解．