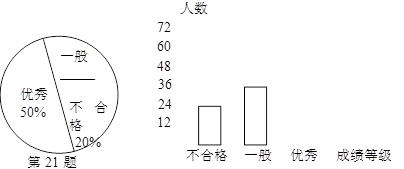题目内容
(11·漳州)(满分14分)如图1,抛物线y=mx2-11mx+24m (m<0) 与x轴交于B、C两点(点B在点C的左侧),抛物线另有一点A在第一象限内,且∠BAC=90°.
(1)填空:OB=_ ▲ ,OC=_ ▲ ;
(2)连接OA,将△OAC沿x轴翻折后得△ODC,当四边形OACD是菱形时,求此时抛物线的解析式;
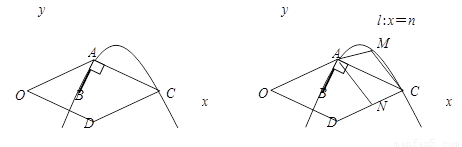 (3)如图2,设垂直于x轴的直线l:x=n与(2)中所求的抛物线交于点M,与CD交于点N,若直线l 沿x轴方向左右平移,且交点M始终位于抛物线上A、C两点之间时,试探究:当n为何值时,四边形AMCN的面积取得最大值,并求出这个最大值.
(3)如图2,设垂直于x轴的直线l:x=n与(2)中所求的抛物线交于点M,与CD交于点N,若直线l 沿x轴方向左右平移,且交点M始终位于抛物线上A、C两点之间时,试探究:当n为何值时,四边形AMCN的面积取得最大值,并求出这个最大值.
解:(1)OB=3,OC=8 ………………4分
(2)连接OD,交OC于点E
∵四边形OACD是菱形
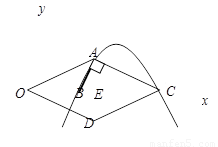 ∴AD⊥OC,OE=EC= ×8=4
∴AD⊥OC,OE=EC= ×8=4
∴BE=4-3=1
又∵∠BAC=90°,
∴△ACE∽△BAE
∴=
∴AE2=BE·CE=1×4
∴AE=2 ………………6分
∴点A的坐标为 (4,2) ………………7分
把点A的坐标 (4,2)代入抛物线y=mx2-11mx+24m,得m=-
 ∴抛物线的解析式为y=-x2+x-12
………………9分
∴抛物线的解析式为y=-x2+x-12
………………9分
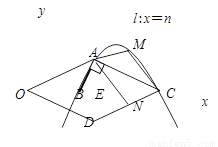
(3)∵直线x=n与抛物线交于点M
∴点M的坐标为 (n,-n2+n-12)
由(2)知,点D的坐标为(4,-2),
则C、D两点的坐标求直线CD的解析式为y=x-4
∴点N的坐标为 (n,n-4)
∴MN=(-n2+n-12)-(n-4)=-n2+5n-8 ………………11分[来源:Zxxk.Com]
∴S四边形AMCN=S△AMN+S△CMN=MN·CE=(-n2+5n-8)×4
=-(n-5)2+9 ………………13分
∴当n=5时,S四边形AMCN=9 ………………14分
【解析】略

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案(11·漳州)(满分8分)某校“我爱学数学”课题学习小组的活动主题是“测量学校旗杆的高度”.以下是该课题小组研究报告的部分记录内容:
| 课题 | 测量学校旗杆的高度 |
| 图示 |
|
| 发言记录 | 小红:我站在远处看旗杆顶端,测得仰角为30° 小亮:我从小红的位置向旗杆方向前进12 m看旗杆顶端,测得仰角为60° 小红:我和小亮的目高都是1.6 m |
请你根据表格中记录的信息,计算旗杆AG的高度.(取1.7,结果保留两个有效数字)