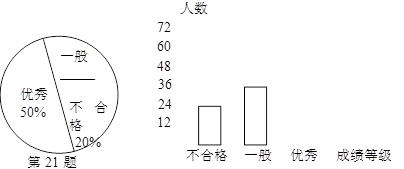题目内容
(11·漳州)(满分13分)如图,直线y=-2x+2与x轴、y轴分别交于A、B两点,将△OAB绕点O逆时针方向旋转90°后得到△OCD.
(1)填空:点C的坐标是(_ ▲ ,_ ▲ ),
点D的坐标是(_ ▲ ,_ ▲ );
(2)设直线CD与AB交于点M,求线段BM的长;
(3)在y轴上是否存在点P,使得△BMP是等腰三角形?若存在,
请求出所有满足条件的点P的坐标;若不存在,请说明理由.
解:(1)点C的坐标是(0,1),点D的坐标是(-2,0) ………………4分
(2)方法一:由(1)可知CD= =,BC=1
又∠1=∠5,∠4=∠3
∴△BMC∽△DOC ………………6分
∴= 即=
∴BM= ………………8分
方法二:设直线CD的解析式为y=kx+b
由(1)得
解得
∴直线CD的解析式为y= x+1
又∠1=∠5,∠BCM=∠DCO
∴△BMC∽△DOC ………………6分
∴= 即=
∴BM= ………………8分
∵ ∴
∴M的坐标为(,) ………………6分
过点M作ME⊥y轴于点E,则ME=,BE=
∴BM= = ………………8分
(3)存在 ………………9分
分两种情况讨论:
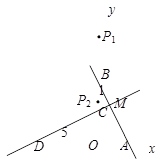
① 以BM为腰时
∵BM=,又点P在y轴上,且BP=BM
此时满足条件的点P有两个,它们是P1 (0,2+)、P2 (0,2-) ……………11分
过点M作ME⊥y轴于点E,∵∠BMC=90°,
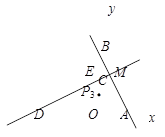
 则△BME∽△BCM
则△BME∽△BCM
∴=
∴BE==
又∵BM=BP
∴PE=BE=
∴BP=
∴OP=2-=
此时满足条件的点P有一个,它是P3 (0,) ……………12分
② 以BM为底时,作BM的垂直平分线,分别交y轴、BM于点P、F,
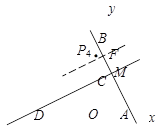 由(2)得∠BMC=90°,
由(2)得∠BMC=90°,
∴PF∥CM
∵F是BM的中点,
∴BP=BC=
∴OP=
此时满足条件的点P有一个,它是P4 (0,)
综上所述,符合条件的点P有四个,它们是:P1 (0,2+)、P2 (0,2-)、P3 (0,)、P4 (0,) ……………13分
解析:略

(11·漳州)(满分8分)某校“我爱学数学”课题学习小组的活动主题是“测量学校旗杆的高度”.以下是该课题小组研究报告的部分记录内容:
| 课题 | 测量学校旗杆的高度 |
| 图示 |
|
| 发言记录 | 小红:我站在远处看旗杆顶端,测得仰角为30° 小亮:我从小红的位置向旗杆方向前进12 m看旗杆顶端,测得仰角为60° 小红:我和小亮的目高都是1.6 m |
请你根据表格中记录的信息,计算旗杆AG的高度.(取1.7,结果保留两个有效数字)