题目内容
【题目】如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.

(1)说明BE=CF的理由;
(2)如果AB=5,AC=3,求AE、BE的长.
【答案】(1)见解析;(2)AE=4,BE=1.
【解析】
(1)连接DB,DC,证明Rt△BED≌Rt△CFD,再运用全等三角形的性质即可证明;
(2).先证明△AED≌△AFD得到AE=AF,设BE=x,则CF=x, 利用线段的和差即可完成解答.
(1)证明:连接BD,CD,
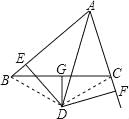
∵ AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∠BED=∠CFD=90°,
∵DG⊥BC且平分BC,
∴BD=CD,
在Rt△BED与Rt△CFD中,
![]() ,
,
∴Rt△BED≌Rt△CFD(HL),
∴BE=CF;
(2)解:在△AED和△AFD中,
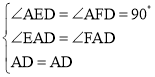
∴△AED≌△AFD(AAS),
∴AE=AF,
设BE=x,则CF=x,
∵AB=5,AC=3,AE=AB﹣BE,AF=AC+CF,
∴5﹣x=3+x,解得:x=1,
∴BE=1,即AE=AB﹣BE=5﹣1=4.

【题目】如图,△ABC的两个外角平分线交于点P,则下列结论正确的是( )
①PA=PC ②BP平分∠ABC ③P到AB,BC的距离相等 ④BP平分∠APC.

A. ①② B. ①④ C. ②③ D. ③④
【题目】某公司生产的某种产品每件成本为40元,经市场调查整理出如下信息:
①该产品90天售量(n件)与时间(第x天)满足一次函数关系,部分数据如下表:
时间(第x天) | 1 | 2 | 3 | 10 | … |
日销售量(n件) | 198 | 196 | 194 | ? | … |
②该产品90天内每天的销售价格与时间(第x天)的关系如下表:
时间(第x天) | 1≤x<50 | 50≤x≤90 |
销售价格(元/件) | x+60 | 100 |
(1)求出第10天日销售量;
(2)设销售该产品每天利润为y元,请写出y关于x的函数表达式,并求出在90天内该产品的销售利润最大?最大利润是多少?(提示:每天销售利润=日销售量×(每件销售价格-每件成本))
(3)在该产品销售的过程中,共有多少天销售利润不低于5400元,请直接写出结果.