题目内容
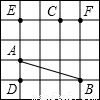
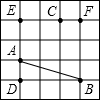 已知如图,每个小方格的边长为1,以A、B、C、D、E、F其中的三个点,能否找到三边长都是无理数三角形?如能,请你在图中连好线;点C到线段AB的距离等于多少?
已知如图,每个小方格的边长为1,以A、B、C、D、E、F其中的三个点,能否找到三边长都是无理数三角形?如能,请你在图中连好线;点C到线段AB的距离等于多少?
分析:因为AE=2,BF=3,AD=3,所以D、E、F点均不符合题目要求,AC=2
,AB=BC=
,故C点符合要求;点C到AB的距离可以根据面积相等法计算.
| 2 |
| 10 |
解答: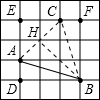 解:连接AC,BC,找到AC中点H,连接BH,
解:连接AC,BC,找到AC中点H,连接BH,
读图可知AC=2
,AB=BC=
,BH=2
,
∵AB=BC,且H为AC中点
∴BH⊥AC,∴△ABC面积为
×AC×BH=4,
设C到AB的距离为x,则
•AB•x=4,
∴x=
,
故△ABC为三边均为无理数的三角形,
C到AB的距离为
.
 解:连接AC,BC,找到AC中点H,连接BH,
解:连接AC,BC,找到AC中点H,连接BH,读图可知AC=2
| 2 |
| 10 |
| 2 |
∵AB=BC,且H为AC中点
∴BH⊥AC,∴△ABC面积为
| 1 |
| 2 |
设C到AB的距离为x,则
| 1 |
| 2 |
∴x=
4
| ||
| 5 |
故△ABC为三边均为无理数的三角形,
C到AB的距离为
4
| ||
| 5 |
点评:本题考查了直角三角形中勾股定理的运用,考查了三角形面积的计算,本题中找出C点是正确解题的关键.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
 已知:如图,每个小方格是边长为1的正方形,则△ABC的周长为
已知:如图,每个小方格是边长为1的正方形,则△ABC的周长为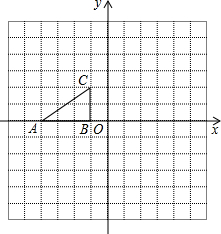 如图,每个小方格都是边长为1个单位的正方形.Rt△ABC 的顶点在格 点上,建立平面直角坐标系后,点A的坐标为(-4,0),点B的坐标为(-1,0).已知Rt△ABC和Rt△A1B1C1关于y轴对称,Rt△A1B1C1和Rt△A2B2C2关于直线y=-2轴对称.
如图,每个小方格都是边长为1个单位的正方形.Rt△ABC 的顶点在格 点上,建立平面直角坐标系后,点A的坐标为(-4,0),点B的坐标为(-1,0).已知Rt△ABC和Rt△A1B1C1关于y轴对称,Rt△A1B1C1和Rt△A2B2C2关于直线y=-2轴对称.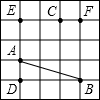 已知如图,每个小方格的边长为1,以A、B、C、D、E、F其中的三个点,能否找到三边长都是无理数三角形?如能,请你在图中连好线;点C到线段AB的距离等于多少?
已知如图,每个小方格的边长为1,以A、B、C、D、E、F其中的三个点,能否找到三边长都是无理数三角形?如能,请你在图中连好线;点C到线段AB的距离等于多少?