Question

【题目】已知抛物线 y ax2 bx c a 0经过点 A2, 0、 B 5, 0.

（1）用含 a 的代数式表示b 、c ；

（2）若点C 6, 4在抛物线上，在抛物线上找一点 P ，使 x 轴恰好平分CAP ，若存在求出点 P ，并求出此时ACP 的面积；

（3）在（2）的条件下，在抛物线的对称轴上是否存在一点Q，使tan AQC 2 ，若存在求出点Q 的坐标，若不存在请说明理由.

Answer 1

【答案】（1）b=-3a, c=-10a (2) P(4，3)；；（3）或

【解析】

（1）把A2, 0、 B 5, 0代入解析式可得方程组，求解可得答案；

（2）将C 6, 4代入，求得函数解析式，设存在点，使x 轴恰好平分CAP，则点P关于X轴的对称点Q在AC上，,且，求出直线AC解析式，再将点Q坐标代入，可得m的值，则得到P（4，3），进而得到三解形ACP的面积；

（3）由 tan AQC 2 得 ，在Rt△ACE中， ，设△ACQ的外接圆圆心为D(m,n),连接AD交圆D于P,则APC＝AQC,∠ACP=90° ，，在Rt△ACP中，，得△ACQ的外接圆直径，半径为5.设△ACQ的外接圆圆心为D(m,n),可得到方程组，解方程组得到D的坐标为D(1,-4)或（3，0），再利用勾股定理解Rt△DHQ，得到QH的长，进而得到点Q的坐标.

（1）把A2, 0、 B 5, 0代入解析式可得：

解得b=-3a, c=-10a

(2) 由点C 6, 4在抛物线上，得

解得，，

故解析式为

如图，设存在点，使x 轴恰好平分CAP，则点P关于X轴的对称点Q在AC上，,且，

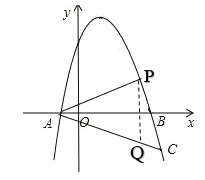
∵A(-2,0),C(6,-4),

∴可得直线AC的解析式为：

∴

解得

∴P(4，3)

∴

（3）如图，过点C作CE⊥x轴于点E，

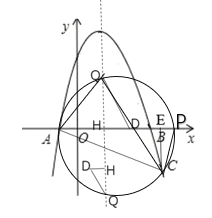
∵ tan AQC 2

∴

∵A(-2,0),C(6,-4),

∴AE=8,CE=4

在Rt△ACE中，

设△ACQ的外接圆圆心为D(m,n),连接AD交圆D于P,则

APC＝AQC,∠ACP=90°，

∴

在Rt△ACP中

∴AP

∴圆D的半径为5

∴AD=DC=5，

∴

解得

当D(1,-4)时，

在Rt△DHQ中，DH=,DQ=5,

∴

∴

当D(3,0)时，

在Rt△DHQ中，DH=,DQ=5,

∴

∴

综上所述，点或.