题目内容
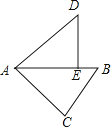
【题目】如图,在等腰直角△ABC中,∠ACB=90°,CO⊥AB于点O,点D、E分别在边AC、BC上,且AD=CE,连结DE交CO于点P,给出以下结论:
①△DOE是等腰直角三角形;②∠CDE=∠COE;③若AC=1,则四边形CEOD的面积为 ![]() ;④AD2+BE2﹣2OP2=2DPPE,其中所有正确结论的序号是
;④AD2+BE2﹣2OP2=2DPPE,其中所有正确结论的序号是
【答案】①②③④
【解析】解:①正确.如图,∵∠ACB=90°,AC=BC,CO⊥AB
∴AO=OB=OC,∠A=∠B=∠ACO=∠BCO=45°,
在△ADO和△CEO中, ,
,
∴△ADO≌△CEO,
∴DO=OE,∠AOD=∠COE,
∴∠AOC=∠DOE=90°,
∴△DOE是等腰直角三角形.故①正确.
②正确.∵∠DCE+∠DOE=180°,
∴D、C、E、O四点共圆,
∴∠CDE=∠COE,故②正确.
③正确.∵AC=BC=1,
∴S△ABC= ![]() ×1×1=
×1×1= ![]() ,S四边形DCEO=S△DOC+S△CEO=S△CDO+S△ADO=S△AOC=
,S四边形DCEO=S△DOC+S△CEO=S△CDO+S△ADO=S△AOC= ![]() S△ABC=
S△ABC= ![]() ,
,
故③正确.
④正确.∵D、C、E、O四点共圆,
∴OPPC=DPPE,
∴2OP2+2DPPE=2OP2+2OPPC=2OP(OP+PC)=2OPOC,
∵∠OEP=∠DCO=∠OCE=45°,∠POE=∠COE,
∴△OPE∽△OEC,
∴ ![]() =
= ![]() ,
,
∴OPOC=OE2 ,
∴2OP2+2DPPE=2OE2=DE2=CD2+CE2 ,
∵CD=BE,CE=AD,
∴AD2+BE2=2OP2+2DPPE,
∴AD2+BE2﹣2OP2=2DPPE.
故④正确.
①正确.由ADO≌△CEO,推出DO=OE,∠AOD=∠COE,由此即可判断.
②正确.由D、C、E、O四点共圆,即可证明.
③正确.由S△ABC= ![]() ×1×1=
×1×1= ![]() ,S四边形DCEO=S△DOC+S△CEO=S△CDO+S△ADO=S△AOC=
,S四边形DCEO=S△DOC+S△CEO=S△CDO+S△ADO=S△AOC= ![]() S△ABC即可解决问题.④正确.由D、C、E、O四点共圆,得OPPC=DPPE,所以2OP2+2DPPE=2OP2+2OPPC=2OP(OP+PC)=2OPOC,由△OPE∽△OEC,得到
S△ABC即可解决问题.④正确.由D、C、E、O四点共圆,得OPPC=DPPE,所以2OP2+2DPPE=2OP2+2OPPC=2OP(OP+PC)=2OPOC,由△OPE∽△OEC,得到 ![]() =
= ![]() ,即可得到2OP2+2DPPE=2OE2=DE2=CD2+CE2 , 由此即可证明.本题考查勾股定理、四点共圆、全等三角形的判定和性质、等腰直角三角形的性质、相似三角形的判定和性质等知识,解题的关键是正确寻找全等三角形,学会利用四点共圆解决问题,题目比较难,用到的知识点比较多.
,即可得到2OP2+2DPPE=2OE2=DE2=CD2+CE2 , 由此即可证明.本题考查勾股定理、四点共圆、全等三角形的判定和性质、等腰直角三角形的性质、相似三角形的判定和性质等知识,解题的关键是正确寻找全等三角形,学会利用四点共圆解决问题,题目比较难,用到的知识点比较多.