题目内容
【题目】如图,四边形ABCD中,∠BAD=110°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为 . 
【答案】140°
【解析】作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,则A′A″即为△AMN的周长最小值。作DA延长线AH,
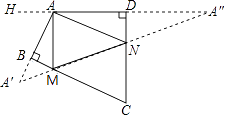
∵∠DAB=110°,
∴∠HAA′=70°,
∴∠AA′M+∠A″=∠HAA′=70°,
∵∠MA′A=∠MAA′,∠NAD=∠A″,且∠MA′A+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2(∠AA′M+∠A″)=2×70°=140°.
【考点精析】本题主要考查了三角形的外角和作轴对称图形的相关知识点,需要掌握三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;画对称轴图形的方法:①标出关键点②数方格,标出对称点③依次连线才能正确解答此题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目