题目内容
一慢车和一快车沿相同路线从A地到B地，所行的路程与时间的函数图象如图所示，试根据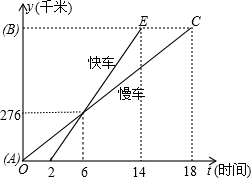
图象，回答下列问题：（1）快车追上慢车需几个小时？
（2）求慢车、快车的速度；
（3）求A、B两地之间的路程．
分析：（1）由图可直接得到快车追上慢车的时间；
（2）从图中得到行至276km时两车所用时间，利用速度=
解答；
（3）求出慢车行驶的函数解析式，将x=18代入解析式，求出y的值即为求A、B两地之间的路程．
（2）从图中得到行至276km时两车所用时间，利用速度=
| 路程 |
| 时间 |
（3）求出慢车行驶的函数解析式，将x=18代入解析式，求出y的值即为求A、B两地之间的路程．
解答：解：（1）快车从慢车出发后2小时出发，6小时时相遇，用了6-2=4小时追上快车；
（2）慢车速度：
=46km/h；快车速度：
=69km/h．
（3）设慢车行驶的解析式为y=kx，
将（6，276）代入解析式得，276=6k，
k=46，解析式为y=46x，
当x=18时，y=46×18=828km．
可见AB之间的距离为828km．
（2）慢车速度：
| 276 |
| 6 |
| 276 |
| 4 |
（3）设慢车行驶的解析式为y=kx，
将（6，276）代入解析式得，276=6k，
k=46，解析式为y=46x，
当x=18时，y=46×18=828km．
可见AB之间的距离为828km．
点评：本题考查了一次函数的应用，由于有两个函数图象，要知道两个函数的交点即为两车相遇点．
练习册系列答案
品学双优卷系列答案
小学期末冲刺100分系列答案
期末复习检测系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
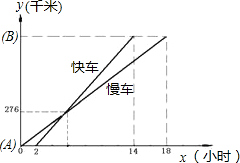所示．请你根据图象，回答下列问题：
间的函数图象如图所示．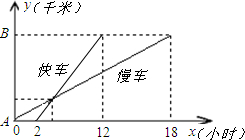
的函数图象如图所示．试根据图象，回答下列问题：
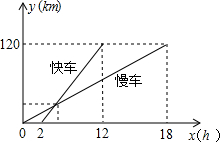数图象如图所示．试根据图象，回答下列问题：