题目内容
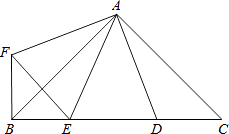
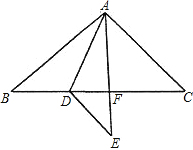
【题目】如图,已知△ABC中,∠B=∠E=40°,∠BAE=60°,且AD平分∠BAE交BC于D.
(1)求证:BD=DE;
(2)若AB=CD,求∠ACD的大小.
【答案】(1)证明见解析;(2)40°
【解析】
(1)要求证:BD=DE可以证明△ABD≌△AED,根据角角边定理就可以证出;
(2)根据AB=AE, AB=CD,得CD=AE,由三角形内角和定理和三角形的外角性质推理可得∠EDC=∠E,则FD=FE,所以CF=AF,再由三角形内角和求出∠ACD.
(1)证明:
∵AD平分∠BAE,
∴∠BAD=∠EAD=30° ,
∵AD=AD,
∵∠B=∠E=40°,
∴△ABD≌△AED ,
∴BD=ED;
(2)解:在△ABD中,
∠ADB=180°﹣∠B﹣∠BAD=110°,
∵△ABD≌△AED,
∴∠ADE=∠ADB=110°,
∵∠ADC=∠B+∠BAD= 70°,
∴∠EDC=∠ADE -∠ADC =110°﹣70°=40°,
∴∠EDC=∠E,
∴FD=FE,
∵AE=AB=CD,
∴EA-EF=DC-DF,
即CF=AF,
∵∠AFC=∠B+∠BAE=60°+40°=100°,
∴∠ACD=![]() (180°-∠AFC)=
(180°-∠AFC)=![]() (180°-100°)= 40°.
(180°-100°)= 40°.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案【题目】林丛同学调查了全班50名同学分别喜欢相声、小品、歌曲、舞蹈节目的情况,并制成下面的统计表:
最喜欢的节目类型 | 划记 | 人数 | 百分比 |
相声 | 正 | 13 | 26% |
小品 | 正正正一 | 21 | 42% |
歌曲 | 正正 | 10 | 28% |
舞蹈 | 正一 | 6 | 12% |
在上表所给的数据中,仅有一类节目的统计是完全正确的,则该项目统计类别是________.
【题目】已知某品牌的饮料有大瓶装与小瓶装之分.某超市花了3800元购进一批该品牌的饮料共1000瓶,其中大瓶和小瓶饮料的进价及售价如下表所示:
大瓶 | 小瓶 | |
进价(元/瓶) | 5 | 2 |
售价(元/瓶) | 7 | 3 |
(1)该超市购进大瓶和小瓶饮料各多少瓶?
(2)在大瓶饮料售出200瓶,小瓶饮料售出100瓶后,商家决定将剩下的小瓶饮料的售价降低0.5元销售,并把其中一定数量的小瓶饮料作为赠品,在顾客一次性购买大瓶饮料时,每满2瓶就送1瓶小瓶饮料,送完即止.超市要使这批饮料售完后获得的利润不低于1250元,那么小瓶饮料作为赠品最多只能送出多少瓶?