题目内容
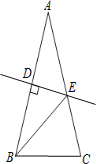
【题目】如图,在△ABC中,AB=AC,,AB的垂直平分线交AB于D,交AC于点E,连接BE,∠EBC=45°,DE=3,求BE的长.
【答案】6.
【解析】
根据已知可得∠ABC=∠C,∠A=∠ABE ,设∠A=x°,利用三角形内角和定理列方程可得∠A=30°,从而在直角△EDB中,利用30°角所对的边是斜边的一半,求得BE的长.
解:∵AB=AC,
∴∠ABC=∠C,
∵DE垂直平分AB,
∴AE=BE ,
∴∠A=∠ABE ,
设∠A=x°,则∠ABC=∠C=(x+45)°在△ABC中,
∵∠A+∠ABC+∠C=180°,
∴ x+x+45+x+45=180°,
解得,x=30 ,∴∠DBE=30°
在直角△EDB中,
∵∠BDE=90°,∠DBE=30°,
∴BE=2DE=6 .

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某校九年级开展“光盘行动”宣传活动,各班级参加该活动的人数统计结果如下表,对于这组统计数据,下列说法中正确的是( )
班级 | 1班 | 2班 | 3班 | 4班 | 5班 | 6班 |
人数 | 52 | 60 | 62 | 54 | 58 | 62 |
A.平均数是58
B.中位数是58
C.极差是40
D.众数是60
【题目】水果市场将120吨水果运往各地商家,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)若全部水果都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节约运费,市场可以调用甲、乙、丙三种车型参与运送(每种车型至少1辆),已知它们的总辆数为16辆,你能通过列方程组的方法分别求出几种车型的辆数吗?