题目内容
在矩形ABCD中,AB=10,BC=12,E为DC的中点,连接BE,作AF⊥BE,垂足为F.
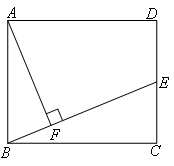
(1)求证:△BEC∽△ABF;
(2)求AF的长.

(1)求证:△BEC∽△ABF;
(2)求AF的长.
(1)证明见解析;(2) .
.
 .
.试题分析:由矩形ABCD中,AB=10,BC=12,E为DC的中点,由勾股定理可求得BE的长,又由AF⊥BE,易证得△ABF∽△BEC,然后由相似三角形的对应边成比例,求得AF的长.
试题解析:(1)证明:在矩形ABCD中,有
∠C=∠ABC=∠ABF+∠EBC=90°,
∵AF⊥BE,∴∠AFB=∠C=90°
∴∠ABF+∠BAF=90°
∴∠BAF=∠EBC
∴△BEC∽△ABF
(2)解:在矩形ABCD中,AB=10,∴CD=AB=10,
∵E为DC的中点,∴CE=5,
又BC=12,在Rt△BEC中,由勾股定理得BE=13,
由△ABF∽△BEC得

即
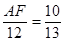 ,解得AF=
,解得AF=
考点: 1.相似三角形的判定与性质;2.勾股定理;3.矩形的性质.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
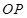 的长.(提示:请先在备用图中画出相应的图形,再求
的长.(提示:请先在备用图中画出相应的图形,再求
 。
。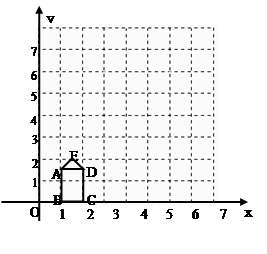
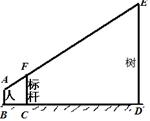
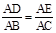 .求证:DE∥BC
.求证:DE∥BC