题目内容
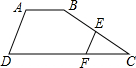 如图,梯形ABCD中,AB∥CD,点E为BC的中点,点F为CD上一点,且CD-AB=2CF,若
如图,梯形ABCD中,AB∥CD,点E为BC的中点,点F为CD上一点,且CD-AB=2CF,若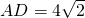 ,则EF等于
,则EF等于
- A.
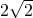
- B.4
- C.2
- D.

A
分析:过B作BH∥AD交DC于H,构造平行四边形,再由已知条件证明EF为一三角形的中位线,求得它所在的三角形的第三边的长也就求得了EF长.
解答:过B作BH∥AD,
∵AB∥CD,
∴四边形ABHD是平行四边形,
∴AB=DH,AD=BH
∵CD-AB=2CF,
∴CD-DH=2CF,
∴CH=2CF,
∴F为CH的中点,
又∵点E为BC的中点,
∴EF为中位线,
∴EF= BH=
BH= AD,
AD,
∵AD=4 ,
,
∴EF=2
故选A.
点评:本题考查的是三角形的中位线等于第三边长的一半及平行四边形的判定及性质,解题的关键是作平行线构造平行四边形.
分析:过B作BH∥AD交DC于H,构造平行四边形,再由已知条件证明EF为一三角形的中位线,求得它所在的三角形的第三边的长也就求得了EF长.
解答:过B作BH∥AD,

∵AB∥CD,
∴四边形ABHD是平行四边形,
∴AB=DH,AD=BH
∵CD-AB=2CF,
∴CD-DH=2CF,
∴CH=2CF,
∴F为CH的中点,
又∵点E为BC的中点,
∴EF为中位线,
∴EF=
 BH=
BH= AD,
AD,∵AD=4
 ,
,∴EF=2

故选A.
点评:本题考查的是三角形的中位线等于第三边长的一半及平行四边形的判定及性质,解题的关键是作平行线构造平行四边形.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
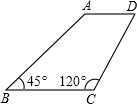 已知,如图,梯形ABCD中,AD∥BC,∠B=45°,∠C=120°,AB=8,则CD的长为( )
已知,如图,梯形ABCD中,AD∥BC,∠B=45°,∠C=120°,AB=8,则CD的长为( )A、
| ||||
B、4
| ||||
C、
| ||||
D、4
|
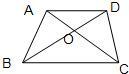 5、已知:如图,梯形ABCD中,AD∥BC,AB=DC,AC、BD相交于点O,那么,图中全等三角形共有
5、已知:如图,梯形ABCD中,AD∥BC,AB=DC,AC、BD相交于点O,那么,图中全等三角形共有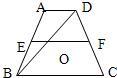 10、如图,梯形ABCD中,AD∥BC,BD为对角线,中位线EF交BD于O点,若FO-EO=3,则BC-AD等于( )
10、如图,梯形ABCD中,AD∥BC,BD为对角线,中位线EF交BD于O点,若FO-EO=3,则BC-AD等于( ) 如图,梯形ABCD中,已知AD∥BC,∠A=90°,AB=7,AD=2,
如图,梯形ABCD中,已知AD∥BC,∠A=90°,AB=7,AD=2,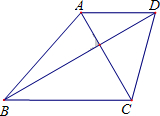 如图,梯形ABCD中,AD∥BC,BC=5,AD=3,对角线AC⊥BD,且∠DBC=30°,求梯形ABCD的高.
如图,梯形ABCD中,AD∥BC,BC=5,AD=3,对角线AC⊥BD,且∠DBC=30°,求梯形ABCD的高.