题目内容
【题目】如图1,是一个长为2m、宽为2n的长方形,沿图中虚线剪成四个完全一样的小长方形,然后按图2的形状拼成一个正方形. 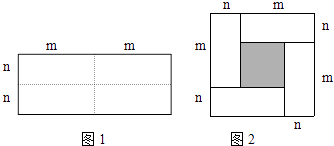
(1)图2中阴影部分的面积为;
(2)用两种不同的方法计算图2中阴影部分的面积,可以得到的等式是(只填序号); ①(m+n)2=m2+2mn+n2 ②(m﹣n)2=m2﹣2mn+n2③(m﹣n)2=(m+n)2﹣4mn
(3)若x﹣y=﹣4,xy= ![]() ,则x+y= .
,则x+y= .
【答案】
(1)(m﹣n)2或(m+n)2﹣4mn
(2)③
(3)±5
【解析】解:(1)图中阴影部分的面积为(m﹣n)2或(m+n)2﹣4mn, 所以答案是:(m﹣n)2或(m+n)2﹣4mn;(2)(m﹣n)2=(m+n)2﹣4mn,
故选③;(3)∵x﹣y=﹣4,xy= ![]() ,
,
∴(x+y)2=(x﹣y)2+4xy=(﹣4)2+4× ![]() =25,
=25,
∴x+y=±5,
所以答案是:±5.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目