题目内容
【题目】如图,在四边形ABCD中,E是BC边的中点,连结DE并延长,交AB的延长线于点F , AB=BF , 添加一个条件,使四边形ABCD是平行四边形,你认为下面四个条件中可选择的是( ) 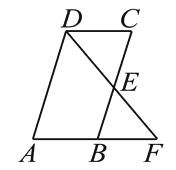
A.AD=BC
B.CD=BF
C.∠A=∠C
D.∠F=∠CDF
【答案】D
【解析】把A、B、C、D四个选项分别作为添加条件进行验证,D为正确选项.
添加D选项,即可证明△DEC≌△FEB , 从而进一步证明DC=BF=AB , 且DC∥AB . ∵∠F=∠CDE
∴CD∥AF
在△DEC与△FEB中,∠DCE=∠EBF , CE=BE(点E为BC的中点),∠CED=∠BEF
∴△DEC≌△FEB
∴DC=BF , ∠C=∠EBF
∴AB∥DC
∵AB=BF
∴DC=AB
∴四边形ABCD为平行四边形
故选D.
【考点精析】解答此题的关键在于理解平行四边形的判定的相关知识,掌握两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目