Question

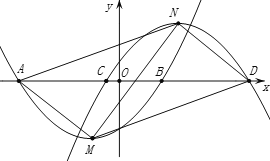
【题目】如图，已知二次函数和二次函数图象的顶点分别为M、N ，与x轴分别相交于A、B两点（点A在点B的左边）和C、D两点（点C在点D的左边），

(1))函数的顶点坐标为 ；当二次函数L1 ，L2 的值同时随着的增大而增大时，的取值范围是 ；

(2)当AD=MN时，求的值，并判断四边形AMDN的形状（直接写出，不必证明）；

(3)当B，C是线段AD的三等分点时，求a的值.

Answer 1

【答案】（1）顶点坐标为M（-1，-2），；（2）四边形AMDN是矩形，理由见解析；（3）

【解析】

（1）把化为顶点式，即可求出顶点坐标；根据图像即可求出次函数L1 ，L2 的值同时随着的增大而增大时，的取值范围；

（2）由两点间的距离公式求出MN的长，用含a的代数式表示出AD的长，根据AD=MN列方程即可求出a的值；由两点间的距离公式可求AN=MD，AM=DN，从而可证四边形AMDN是平行四边形，又AD=MN，所以可证四边形AMDN是矩形；

（3）当B，C是线段AD的三等分点时，分两种情况，根据两点间的距离公式求解：①点C在点B的左边，②点B在点C的左边.

（1）∵

∴，

∴顶点坐标为M（-1，-2）；

∵M（-1，-2），N（2，2），

∴当时， L1 的y值随着x的增大而增大，当时，L2的y值随着x的增大而增大.

∴的取值范围是 .

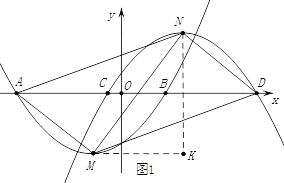
（2）如图1，=5，

当y=0时，即，解得，，

当y=0时，即，，，

∴AD=（）-（）=img src="http://thumb.zyjl.cn/Upload/2019/10/22/08/84bfb46e/SYS201910220806224121870752_DA/SYS201910220806224121870752_DA.019.png" width="56" height="36" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />，

当AD=MN时，即=5，解得a=2 .

当 a=2时，

=-2，=3，

∵AN=,DM=,

∴AN=DM,

∵AM=,DN=,

∴AM=DN,

∴四边形AMDN是平行四边形，

∵AD=3-(-2)=5,MN=5,

∴AD=MN,

∴四边形AMDN是矩形 ;

（3）当B，C是线段AD的三等分点时，存在以下两种情况：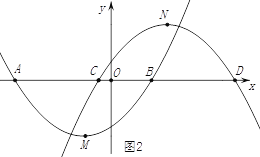

①点C在点B的左边，如图2，BC=（）-（）=，AC=BD=3 ，

即 =3，解得 ;

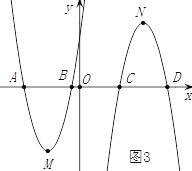
②点B在点C的左边，如图3，CB=（）-（）=，AB=CD= ，

即=，解得 .