题目内容
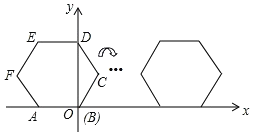
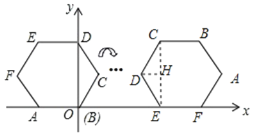
【题目】如图,将正六边形ABCDEF放置在直角坐标系内,A(﹣2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2020次翻转之后,点C的坐标是_____.
【答案】(4038,2![]() )
)
【解析】
先求出开始时点C的横坐标为![]() OC=1,根据正六边形的特点,每6次翻转为一个循环组循环,用2020除以6,根据商和余数的情况确定出点C的位置,然后求出翻转B前进的距离,连接CE,过点D作DH⊥CE于H,则CE⊥EF,∠CDH=∠EDH=60°,CH=EH,求出CE=2CH=2×CDsin60°=2
OC=1,根据正六边形的特点,每6次翻转为一个循环组循环,用2020除以6,根据商和余数的情况确定出点C的位置,然后求出翻转B前进的距离,连接CE,过点D作DH⊥CE于H,则CE⊥EF,∠CDH=∠EDH=60°,CH=EH,求出CE=2CH=2×CDsin60°=2![]() ,即可得出点C的坐标.
,即可得出点C的坐标.
∵六边形ABCDEF为正六边形,
∴∠AOC=120°,
∴∠DOC=120°﹣90°=30°,
∴开始时点C的横坐标为:![]() OC=
OC=![]() ×2=1,
×2=1,
∵正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,
∴每6次翻转为一个循环组循环,
∵2020÷6=336…4,
∴为第336循环组的第4次翻转,点C在开始时点E的位置,如图所示:
∵A(﹣2,0),
∴AB=2,
∴翻转B前进的距离=2×2020=4040,
∴翻转后点C的横坐标为:4040﹣2=4038,
连接CE,过点D作DH⊥CE于H,则CE⊥EF,∠CDH=∠EDH=60°,CH=EH,
∴CE=2CH=2×CDsin60°=2×2×![]() =2
=2![]() ,
,
∴点C的坐标为(4038,2![]() ),
),
故答案为:(4038,2![]() ).
).

练习册系列答案
相关题目