题目内容
【题目】如图1,在△ABC中,∠B=90°,∠A=30°,AC=2.
(1)将△ABC绕点C顺时针旋转120°得△A′B′C.①求点B旋转经过的路径长;②求线段BB′的长;
(2)如图2,过点C作AC的垂线与AB的延长线交于点D,将△ACD绕点C顺时针旋转90°得△A′CD′.在图2中画出线段AD绕点C旋转所形成的图形(用阴影表示),并求出该图形的面积.

【答案】(1)![]() π;
π;![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)①由旋转的性质可知∠BCB′=120°,然后由扇形的弧长公式即可求得点B旋转经过的路径长;②由特殊锐角三角函数值可求得BB′的长;
(2)首先画出图形,然后根据S1=S2,可求得S1+S4的面积,然后再利用扇形面积-等边三角形ECD′的面积,从而可求得答案.
试题解析:(1)①∵AC=2,∠B=90°,∠A=30°,
∴BC=1.
∴点B旋转的路径=![]() ×2π×12=
×2π×12=![]() π;
π;
②如下图所示:
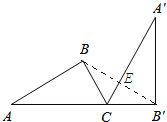
在△BCB′中,CB=CB′,∠BCB′=120°,AC⊥BB′
∴sin∠CBE=![]() .
.
∴BE=![]() .
.
∴BB′=![]() ;
;
(2)如图所示:

∵S1=S2,
∴S2+S4=S1+S4=![]() π(AC2-BC2)=
π(AC2-BC2)=![]() π(22-12)=
π(22-12)=![]() π.
π.
在Rt△ABD中,DC=ACtan30°=![]() ,
,
S3=![]() ×π×(
×π×(![]() )2-
)2-![]() ×
×![]() ×1=
×1=![]() π-
π-![]() ,
,
∴S2+S3+S4=![]() π+
π+![]() π-
π-![]() =
=![]() .
.

练习册系列答案
相关题目