��Ŀ����
��ƽ��ֱ������ϵxOy�У�һ�κ���y=2x+2��ͼ����x�ύ��A����y�ύ�ڵ�C����B������Ϊ��a��0����������a��0����ֱ��l������M��0��m����0��m��2��������x��ƽ�У�����ֱ��AC��BC�ֱ��ཻ�ڵ�D��E��P����y���ϣ�P������C�㣩����PE=CE��ֱ��PD��x�ύ�ڵ�Q������PA��
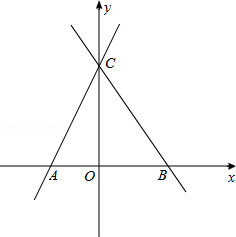
��1��д��A��C��������ꣻ
��2����0��m��1ʱ������PAQ����PΪ����ı��������Σ�ע������HNK����HN=2HK����ơ�HNKΪ��HΪ����ı��������Σ������m��ֵ��
��3����1��m��2ʱ���Ƿ����ʵ��m��ʹCD•AQ=PQ•DE�����ܣ����m��ֵ���ú�a�Ĵ���ʽ��ʾ���������ܣ���˵�����ɣ�

��1��д��A��C��������ꣻ
��2����0��m��1ʱ������PAQ����PΪ����ı��������Σ�ע������HNK����HN=2HK����ơ�HNKΪ��HΪ����ı��������Σ������m��ֵ��
��3����1��m��2ʱ���Ƿ����ʵ��m��ʹCD•AQ=PQ•DE�����ܣ����m��ֵ���ú�a�Ĵ���ʽ��ʾ���������ܣ���˵�����ɣ�
�⣺��1����ֱ�߽���ʽy=2x+2�У���y=0����x=��1��x=0����y=2��
��A����1��0����C��0��2����
��2����0��m��1ʱ�������⻭��ͼ�Σ���ͼ1��
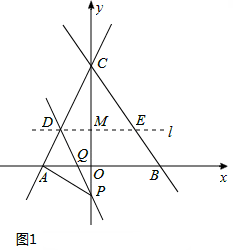
��PE=CE����ֱ��l���߶�PC�Ĵ�ֱƽ���ߡ�
��MC=MP��
��C��0��2����M��0��m������P��0��2m��2����
��ֱ��l��y=2x+2���ڵ�D��
��y=m����x=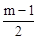 ����D��
����D��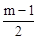 ��m����
��m����
��ֱ��DP�Ľ���ʽΪy=kx+b������
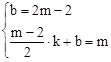 ����ã�
����ã�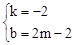 ��
��
��ֱ��DP�Ľ���ʽΪ��y=��2x+2m��2��
��y=0����x=m��1����Q��m��1��0����
��֪��PAQ����PΪ����ı��������Σ���ͼ��֪��PA=2PQ��
��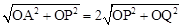 ����
����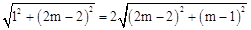 ��
��
�����ã�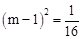 ��
��
��ã�m=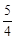 ��
��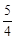 ��1���������⣬��ȥ����m=
��1���������⣬��ȥ����m=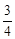 ��
��
��m=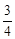 ��
��
��3����1��m��2ʱ���������ʵ��m��ʹCD•AQ=PQ•DE��
�����⻭��ͼ�Σ���ͼ2��
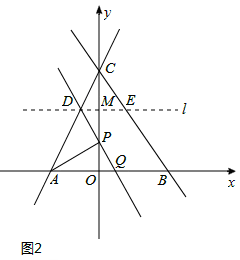
�ɣ�2����֪��OQ=m��1��OP=2m��2��
�ɹ��ɶ����ã�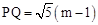 ��
��
��A����1��0����Q��m��1��0����B��a��0����
��AQ=m��AB=a+1��
��OA=1��OC=2���ɹ��ɶ����ã�CA=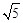 ��
��
��ֱ��l��x�ᣬ���CDE�ס�CAB��
��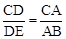 ��
��
�֡�CD•AQ=PQ•DE����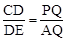 ��
��
��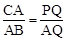 ����
����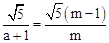 ����ã�
����ã�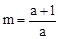 ��
��
��1��m��2���൱0��a��1ʱ��m��2��m�����ڣ���a��1ʱ��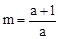 ��
��
�൱1��m��2ʱ����a��1�������ʵ��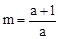 ��ʹCD•AQ=PQ•DE����0��a��1����m�����ڡ�
��ʹCD•AQ=PQ•DE����0��a��1����m�����ڡ�
��A����1��0����C��0��2����
��2����0��m��1ʱ�������⻭��ͼ�Σ���ͼ1��

��PE=CE����ֱ��l���߶�PC�Ĵ�ֱƽ���ߡ�
��MC=MP��
��C��0��2����M��0��m������P��0��2m��2����
��ֱ��l��y=2x+2���ڵ�D��
��y=m����x=
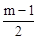 ����D��
����D��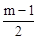 ��m����
��m������ֱ��DP�Ľ���ʽΪy=kx+b������
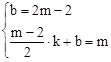 ����ã�
����ã�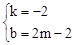 ��
����ֱ��DP�Ľ���ʽΪ��y=��2x+2m��2��
��y=0����x=m��1����Q��m��1��0����
��֪��PAQ����PΪ����ı��������Σ���ͼ��֪��PA=2PQ��
��
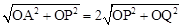 ����
����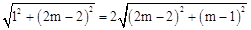 ��
�������ã�
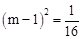 ��
����ã�m=
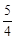 ��
��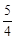 ��1���������⣬��ȥ����m=
��1���������⣬��ȥ����m=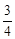 ��
����m=
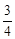 ��
����3����1��m��2ʱ���������ʵ��m��ʹCD•AQ=PQ•DE��
�����⻭��ͼ�Σ���ͼ2��

�ɣ�2����֪��OQ=m��1��OP=2m��2��
�ɹ��ɶ����ã�
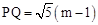 ��
����A����1��0����Q��m��1��0����B��a��0����
��AQ=m��AB=a+1��
��OA=1��OC=2���ɹ��ɶ����ã�CA=
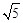 ��
����ֱ��l��x�ᣬ���CDE�ס�CAB��
��
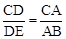 ��
���֡�CD•AQ=PQ•DE����
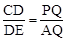 ��
����
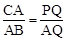 ����
����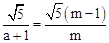 ����ã�
����ã�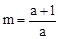 ��
����1��m��2���൱0��a��1ʱ��m��2��m�����ڣ���a��1ʱ��
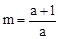 ��
���൱1��m��2ʱ����a��1�������ʵ��
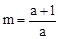 ��ʹCD•AQ=PQ•DE����0��a��1����m�����ڡ�
��ʹCD•AQ=PQ•DE����0��a��1����m�����ڡ������������1������һ�κ���ͼ���ϵ������������⣻
��2����ͼ1��ʾ������ؼ��������P����Q�����꣬Ȼ������PA=2PQ���з�����⡣
��3����ͼ2��ʾ���������������Σ�����֪�ı���ʽת��Ϊ��
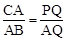 ���ݴ��з������m��ֵ��
���ݴ��з������m��ֵ��
��ϰ��ϵ�д�
�����Ŀ
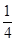 DC������
DC������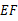 ���ӳ���
���ӳ���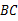 ���ӳ����ڵ�
���ӳ����ڵ�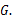
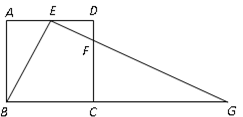
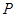 ���߶�
���߶�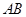 �Ļƽ�ָ�㣬
�Ļƽ�ָ�㣬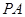 ��
�� ����
����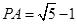 ����
����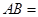 ����������
����������
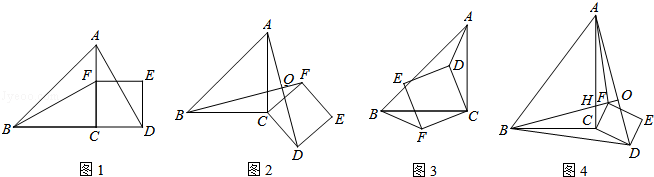
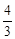 ��CF=1��BF��AC�ڵ�H����AD�ڵ�O������BD��AF����BD2+AF2��ֵ��
��CF=1��BF��AC�ڵ�H����AD�ڵ�O������BD��AF����BD2+AF2��ֵ�� ABCD�У�AB��6��AD��9����BAD��ƽ���߽�BC�ڵ�E��DC���ӳ����ڵ�F, BG��AE������ΪG����BG��4
ABCD�У�AB��6��AD��9����BAD��ƽ���߽�BC�ڵ�E��DC���ӳ����ڵ�F, BG��AE������ΪG����BG��4 �����CEF�������
�����CEF�������
