题目内容
如图，在梯形ABCD中，∠C=45°，∠BAD=∠B=90°，AD=3，CD=2
，M为BC上一动点，则△AMD周长的最小值为______．
| 2 |
过D作DE⊥B以C于E，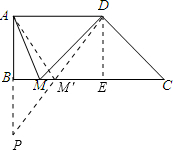
在RT△CDE中，∠C=45°，CD=2
，
∴DE=2，
∴AB=2，
延长AB到P，使BP=AB=2，
连接PD交BC于M′，
PD=
=5，
则△AMD的周长最小值：AD+DM′+AM′=AD+PD=8．
故答案为8．
在RT△CDE中，∠C=45°，CD=2
| 2 |
∴DE=2，
∴AB=2，
延长AB到P，使BP=AB=2，
连接PD交BC于M′，
PD=
| AD2+AP2 |
则△AMD的周长最小值：AD+DM′+AM′=AD+PD=8．
故答案为8．
练习册系列答案
名校课堂系列答案
相关题目
