题目内容
【题目】如图,点A,B,C,D是直径为AB的⊙O上的四个点,C是劣弧 ![]() 的中点,AC与BD交于点E.
的中点,AC与BD交于点E. 
(1)求证:DC2=CEAC;
(2)若AE=2,EC=1,求证:△AOD是正三角形;
(3)在(2)的条件下,过点C作⊙O的切线,交AB的延长线于点H,求△ACH的面积.
【答案】
(1)证明:∵C是劣弧 ![]() 的中点,
的中点,
∴∠DAC=∠CDB,
∵∠ACD=∠DCE,
∴△ACD∽△DCE,
∴ ![]() =
= ![]() ,
,
∴DC2=CEAC
(2)证明:∵AE=2,EC=1,
∴AC=3,
∴DC2=CEAC=1×3=3,
∴DC= ![]() ,
,
连接OC、OD,如图所示:
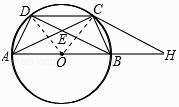
∵C是劣弧 ![]() 的中点,
的中点,
∴OC平分∠DOB,BC=DC= ![]() ,
,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴AB= ![]() =2
=2 ![]() ,
,
∴OB=OC=OD=DC=BC= ![]() ,
,
∴△OCD、△OBC是正三角形,
∴∠COD=∠BOC=∠OBC=60°,
∴∠AOD=180°﹣2×60°=60°,
∵OA=OD,
∴△AOD是正三角形
(3)解:∵CH是⊙O的切线,∴OC⊥CH,
∵∠COH=60°,
∴∠H=30°,
∵∠BAC=90°﹣60°=30°,
∴∠H=∠BAC,
∴AC=CH=3,
∵AH=3 ![]() ,AH上的高为BCsin60°=
,AH上的高为BCsin60°= ![]() ,
,
∴△ACH的面积= ![]() ×3
×3 ![]() ×
× ![]() =
= ![]()
【解析】(1)由圆周角定理得出∠DAC=∠CDB,证明△ACD∽△DCE,得出对应边成比例,即可得出结论;(2)求出DC= ![]() ,连接OC、OD,如图所示:证出BC=DC=
,连接OC、OD,如图所示:证出BC=DC= ![]() ,由圆周角定理得出∠ACB=90°,由勾股定理得出AB=
,由圆周角定理得出∠ACB=90°,由勾股定理得出AB= ![]() =2
=2 ![]() ,得出OB=OC=OD=DC=BC=
,得出OB=OC=OD=DC=BC= ![]() ,证出△OCD、△OBC是正三角形,得出∠COD=∠BOC=∠OBC=60°,求出∠AOD=60°,即可得出结论;(3)由切线的性质得出OC⊥CH,求出∠H=30°,证出∠H=∠BAC,得出AC=CH=3,求出AH和高,由三角形面积公式即可得出答案.
,证出△OCD、△OBC是正三角形,得出∠COD=∠BOC=∠OBC=60°,求出∠AOD=60°,即可得出结论;(3)由切线的性质得出OC⊥CH,求出∠H=30°,证出∠H=∠BAC,得出AC=CH=3,求出AH和高,由三角形面积公式即可得出答案.

 智慧小复习系列答案
智慧小复习系列答案






