题目内容
【题目】如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点,若CF=1,FD=2,则BC的长为【 】

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B。
【解析】过点E作EM⊥BC于M,交BF于N。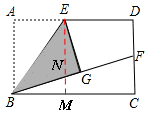
∵四边形ABCD是矩形,∴∠A=∠ABC=90°,AD=BC,
∵∠EMB=90°,∴四边形ABME是矩形。∴AE=BM,
由折叠的性质得:AE=GE,∠EGN=∠A=90°,∴EG=BM。
∵∠ENG=∠BNM,∴△ENG≌△BNM(AAS)。∴NG=NM。
∵E是AD的中点,CM=DE,∴AE=ED=BM=CM。
∵EM∥CD,∴BN:NF=BM:CM。∴BN=NF。∴NM=![]() CF=
CF=![]() 。∴NG=
。∴NG=![]() 。
。
∵BG=AB=CD=CF+DF=3,∴BN=BG﹣NG=3﹣![]() 。∴BF=2BN=5
。∴BF=2BN=5
∴![]() 。故选B。
。故选B。

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目