题目内容
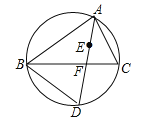
【题目】如图，点E是△ABC的内心，AE的延长线与BC相交于点F，与△ABC的外接圆相交于点D
（1）求证：△BFD∽△ABD；
（2）求证：DE=DB．
【答案】（1）证明见解析；（2）证明见解析．
【解析】
试题分析：（1）先根据内心的性质得出∠BAD=∠CAD，再由圆周角定理得出∠CAD=∠CBD，故可得出∠BAD=∠CBD，进而可得出结论；
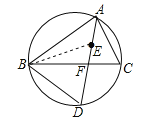
（2）连接BE，根据点E是△ABC的内心得出∠ABE=∠CBE．由∠CBD=∠BAD可得出∠BAD+∠ABE=∠CBE+∠CBD，进而可得出结论．
试题解析：（1）证明：∵点E是△ABC的内心，∴∠BAD=∠CAD．
∵∠CAD=∠CBD，∴∠BAD=∠CBD．
∵∠BDF=∠ADB，∴△BFD∽△ABD；
（2）证明：连接BE，∵点E是△ABC的内心，∴∠ABE=∠CBE．
又∵∠CBD=∠BAD，∴∠BAD+∠ABE=∠CBE+∠CBD．
∵∠BAD+∠ABE=∠BED，∠CBE+∠CBD=∠DBE，即∠DBE=∠BED，∴DE=DB．
练习册系列答案
名校课堂系列答案
相关题目
