题目内容
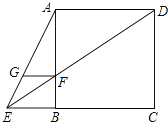
【题目】如图,在△ABC中,∠ACB=90°,AB=5,tanA= ![]() ,将△ABC沿直线l翻折,恰好使点A与点B重合,直线l分别交边AB、AC于点D、E;
,将△ABC沿直线l翻折,恰好使点A与点B重合,直线l分别交边AB、AC于点D、E; 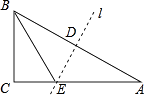
(1)求△ABC的面积;
(2)求sin∠CBE的值.
【答案】
(1)解:∵∠ACB=90°,tanA= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴AC=2BC,
在Rt△ABC中,BC2+AC2=AB2,
即BC2+4BC2=25,
解得BC= ![]() ,
,
所以,AC=2 ![]() ,
,
△ABC的面积= ![]() ACBC=
ACBC= ![]() ×
× ![]() ×2
×2 ![]() =5
=5
(2)解:设CE=x,则AE=AC﹣CE=2 ![]() ﹣x,
﹣x,
∵△ABC沿直线l翻折点A与点B重合,
∴BE=AE=2 ![]() ﹣x,
﹣x,
在Rt△BCE中,BC2+CE2=BE2,
即 ![]() 2+x2=(2
2+x2=(2 ![]() ﹣x)2,
﹣x)2,
解得x= ![]() ,
,
所以,CE= ![]() ,
,
BE=2 ![]() ﹣x=2
﹣x=2 ![]() ﹣
﹣ ![]() =
= ![]() ,
,
所以,sin∠CBE= ![]() =
= ![]() =
= ![]()
【解析】(1)根据∠A的正切用BC表示出AC,再利用勾股定理列方程求出BC,再求出AC,然后根据直角三角形的面积公式列式计算即可得解;(2)设CE=x,表示出AE,再根据翻折变换的性质可得BE=AE,然后列方程求出x,再利用锐角的正弦等于对边比斜边列式计算即可得解.
【考点精析】根据题目的已知条件,利用翻折变换(折叠问题)的相关知识可以得到问题的答案,需要掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.

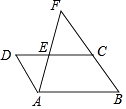
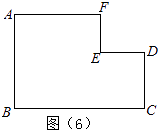
【题目】Word文本中的图形,在图形格式中大小菜单下显示有图形的绝对高度和绝对宽度,同一个图形随其放置方向的变化,所显示的绝对高度和绝对宽度也随之变化.如图①、②、③是同一个三角形以三条不同的边水平放置时,它们所显示的绝对高度和绝对宽度如下表,现有△ABC,已知AB=AC,当它以底边BC水平放置时(如图④),它所显示的绝对高度和绝对宽度如下表,那么当△ABC以腰AB水平放置时(如图⑤),它所显示的绝对高度和绝对宽度分别是( ) 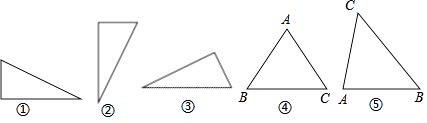
图形 | 图① | 图② | 图③ | 图④ | 图⑤ |
绝对高度 | 1.50 | 2.00 | 1.20 | 2.40 | ? |
绝对宽度 | 2.00 | 1.50 | 2.50 | 3.60 | ? |
A.3.60和2.40
B.2.56和3.00
C.2.56和2.88
D.2.88和3.00
【题目】为了解高邮市6000名九年级学生英语口语考试成绩的情况,从中随机抽取了部分学生的成绩(满分30分,得分均为整数),制成下表:
分数段(x分) | x≤10 | 11≤x≤15 | 16≤x≤20 | 21≤x≤25 | 26≤x≤30 |
人 数 | 10 | 15 | 35 | 112 | 128 |
(1)本次抽样调查共抽取了名学生;
(2)若用扇形统计图表示统计结果,则分数段为x≤10的人数所对应扇形的圆心角为°;
(3)学生英语口语考试成绩的众数落在11≤x≤15的分数段内;(填“会”或“不会”)
(4)若将26分以上(含26)定为优秀,请估计该区九年级考生成绩为优秀的人数.