题目内容
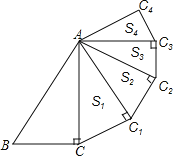
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,以点
,以点![]() 为圆心、2为半径画圆,点
为圆心、2为半径画圆,点![]() 是
是![]() 上任意一点,连接
上任意一点,连接![]() ,
,![]() .将
.将![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]()
(1)当![]() 与
与![]() 相切时,
相切时,
①求证:![]() 是
是![]() 的切线;
的切线;
②求点![]() 到
到![]() 的距离.
的距离.
(2)连接![]() ,
,![]() ,当
,当![]() 的面积最大时,点
的面积最大时,点![]() 到
到![]() 的距离为 .
的距离为 .![]()
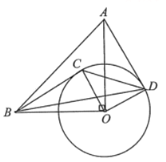
【答案】(1)①见解析,②点C到OB的距离是![]() ;(2)
;(2)![]() .
.
【解析】
(1)①先证明△BOC≌△AOD,则∠BCO=∠ADO=90°,BC是⊙O的切线;
②过点C作CE⊥OB,根据勾股定理得BC=2![]() ,由△BCO的面积公式可得OBCE=BCOC,求得CE=
,由△BCO的面积公式可得OBCE=BCOC,求得CE=![]() ;
;
(2)当点C在⊙O上运动到△BCD是等腰三角形,且BO的延长线与CD垂直位置时,△BCD的面积最大(如图2),由等腰直角三角形的性质可求得OF=![]() ,则点B到CD的距离为4+
,则点B到CD的距离为4+![]() .
.
(1)①证明:∵AD与⊙O相切,∴∠ADO=90°.
∵∠AOB=∠COD=90°,
∴∠AOB-∠AOC=∠COD-∠AOC,即∠COB=∠AOD,
∵OB=OA,OC=OD,
∴△BOC≌△AOD.
∴∠BCO=∠ADO=90°.
∴BC是⊙O的切线.
②过点C作CE⊥OB,垂足为E,则CE即为点C到OB的距离.
在Rt△BOC中,∵OB=4,OC=2,
∴![]() ,
,
∴OBCE=BCOC,即4CE=2![]() ,CE=
,CE=![]() .
.
∴点C到OB的距离是![]() .
.

(2)当点C在⊙O上运动到△BCD是等腰三角形,且BO的延长线与CD垂直位置时,
△BCD的面积最大(如图2),此时OB=4,OC=OD=2,
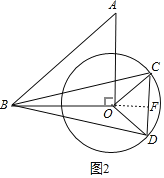
∵△COD是等腰直角三角形,
∴OF=OCsin45°=2×![]() =
=![]() ,
,
∴BF=4+![]() .
.

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案【题目】随着生活水平的提高,人们对空气质量的要求也越来越高。为了了解![]() 月中旬长春市城区的空气质量情况,某校“综合实践环境调查”小组,从天气预报网抽取了朝阳区和南关区这两个城区
月中旬长春市城区的空气质量情况,某校“综合实践环境调查”小组,从天气预报网抽取了朝阳区和南关区这两个城区![]() 年
年![]() 月
月![]() 日——
日——![]() 年
年![]() 月
月![]() 日的空气质量指数,作为样本进行统计,过程如下,请补充完整.
日的空气质量指数,作为样本进行统计,过程如下,请补充完整.
收集数据
朝阳区 |
|
|
|
|
|
|
|
|
|
|
南关区 |
|
|
|
|
|
|
|
|
|
|
整理、描述数据
按下表整理、描述这两城区空气质量指数的数据.
空气质量 | 优 | 良 | 轻微污染 | 中度污染 | 重度污染 |
朝阳区 | |||||
南关区 |
|
|
|
|
|
(说明:空气质量指数![]() 时,空气质量为优;
时,空气质量为优;![]() 空气质量指数
空气质量指数![]() 时,空气质量为良;
时,空气质量为良;![]() 空气质量指数
空气质量指数![]() 时,空气质量为轻微污染;
时,空气质量为轻微污染;![]() 空气质量指数
空气质量指数![]() 时,空气质量为中度污染;
时,空气质量为中度污染;![]() 空气质量指数
空气质量指数![]() 时,空气质量为重度污染.)
时,空气质量为重度污染.)
分析数据
两城区的空气质量指数的平均数、中位数、方差如下表所示.
城区 | 平均数 | 中位数 | 方差 |
朝阳区 |
|
|
|
南关区 |
|
|
请将以上两个表格补充完整.
得出结论可以推断出哪个城区这十天中空气质量情况比较好?请至少从两个不同的角度说明推断的合理性.