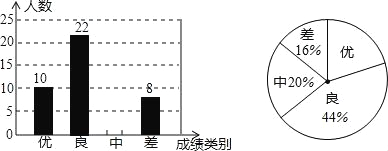
题目内容
【题目】(本小题满分10分)已知二次函数![]()
(1)当![]() 时,函数值
时,函数值![]() 随
随![]() 的增大而减小,求
的增大而减小,求![]() 的取值范围。
的取值范围。
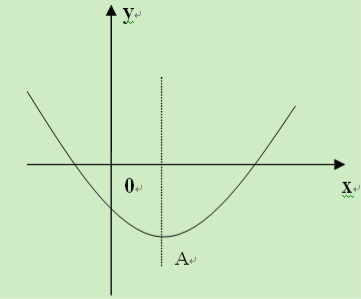
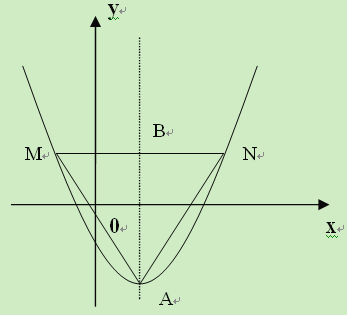
(2)以抛物线![]() 的顶点
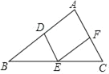
的顶点![]() 为一个顶点作该抛物线的内接正三角形
为一个顶点作该抛物线的内接正三角形![]() (
(![]() ,
,![]() 两点在抛物线上),请问:△
两点在抛物线上),请问:△![]() 的面积是与
的面积是与![]() 无关的定值吗?若是,请求出这个定值;若不是,请说明理由。
无关的定值吗?若是,请求出这个定值;若不是,请说明理由。
(3)若抛物线![]() 与
与![]() 轴交点的横坐标均为整数,求整数
轴交点的横坐标均为整数,求整数![]() 的值。
的值。
【答案】解:(1)∵![]()
∴由题意得,![]() ·······················································(3分)
·······················································(3分)
(2)根据抛物线和正三角形的对称性,可知![]() 轴,设抛物线的对称轴与
轴,设抛物线的对称轴与![]() 交于点
交于点![]() ,则
,则![]() 。设
。设![]()
∴![]()
又![]()
![]()
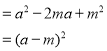
∴![]() ∴
∴![]()
∴![]() ,
,![]()
∴![]() 定值···························································(3分)
定值···························································(3分)
(3)令![]() ,即
,即![]() 时,有
时,有
![]()
由题意,![]() 为完全平方数,令
为完全平方数,令![]()
即![]()
∵![]() 为整数, ∴
为整数, ∴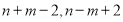 的奇偶性相同
的奇偶性相同
∴![]() 或
或![]()
解得![]() 或
或![]()
综合得![]() ····························································(4分)
····························································(4分)
【解析】略

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
【题目】某校九年级(8)课外活动设置了如图所示的翻牌游戏,每次抽奖翻开一个数字,考虑“第一个人中奖排球”的机会.
正面
1 | 2 | 3 |
4 | 5 | 6 |
7 | 8 | 9 |
反面
排球 | 钢笔 | 图书 |
铅笔 | 空门 | 书包 |
球拍 | 小刀 | 篮球 |
(1)如果用实验进行估计,但制作翻奖牌没有材料,那么你有什么简便的模拟实验方法?
(2)如果不做实验,你能估计“第一个人中奖排球”的机会是多少?