题目内容
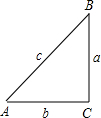 如图,在△ABC中,∠C=90°,角A、B、C的对边分别为a、b、c,设△ABC的面积为s,周长的一半为l.
如图,在△ABC中,∠C=90°,角A、B、C的对边分别为a、b、c,设△ABC的面积为s,周长的一半为l.
(1)填写表:
| 三边a、b、c | l-a | l-b | s |
| 3、4、5 | 3 | 2 | 6 |
| 5、12、13 | |||
| 8、15、17 |
解:(1)填表如下:
(2)m、n与s之间有如下关系:s=mn.
证明:在△ABC中,∠C=90°,s= ab.
ab.
m=l-a=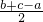 ,
,
n=l-b=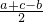 ,
,
∴mn=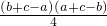 ,
,
即mn= =
=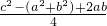 ,
,
又a2+b2=c2,
∴mn=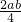 ,
,
∴s=mn.
分析:(1)利用三角形的面积及周长的计算方法求得图中未知数据即可;
(2)根据上题求得的数据猜想三者之间的关系并利用三角形的面积的计算方法证明即可.
点评:本题考查了勾股定理的知识,解题的关键是根据题目提供的信息猜想得到三者之间的关系.
| 三边a、b、c | l-a | l-b | s |
| 3、4、5 | 3 | 2 | 6 |
| 5、12、13 | 10 | 3 | 30 |
| 8、15、17 | 12 | 5 | 60 |
证明:在△ABC中,∠C=90°,s=
 ab.
ab.m=l-a=
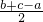 ,
,n=l-b=
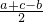 ,
,∴mn=
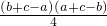 ,
,即mn=
 =
=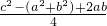 ,
,又a2+b2=c2,
∴mn=
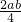 ,
,∴s=mn.
分析:(1)利用三角形的面积及周长的计算方法求得图中未知数据即可;
(2)根据上题求得的数据猜想三者之间的关系并利用三角形的面积的计算方法证明即可.
点评:本题考查了勾股定理的知识,解题的关键是根据题目提供的信息猜想得到三者之间的关系.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 20、如图,在△ABC中,∠BAC=45°,现将△ABC绕点A逆时针旋转30°至△ADE的位置,使AC⊥DE,则∠B=
20、如图,在△ABC中,∠BAC=45°,现将△ABC绕点A逆时针旋转30°至△ADE的位置,使AC⊥DE,则∠B= 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为 2、如图,在△ABC中,DE∥BC,那么图中与∠1相等的角是( )
2、如图,在△ABC中,DE∥BC,那么图中与∠1相等的角是( ) 如图,在△ABC中,AB=AC,且∠A=100°,∠B=
如图,在△ABC中,AB=AC,且∠A=100°,∠B=