题目内容
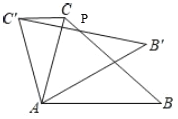
【题目】如图，在同一平面内，将△ABC绕点A旋转到△AB′C′的位置，使得CC′∥AB，BC与 B′C′交于点P，此时∠BPB′＝25°，则∠CAB的大小为_____．
【答案】77.5°
【解析】
根据旋转的性质可得∠BAB′＝∠CAC′，∠B＝∠B′，AC=AC′，根据两直线平行，内错角相等求出∠C′CA＝∠CAB，由三角形内角和定理可求得∠BAB′＝∠BPB′＝25°，从而可得∠CAC′＝25°，然后利用等腰三角形两底角相等求出∠ACC′，继而可求得答案.
∵CC′∥AB，
∴∠C′CA＝∠CAB，
又∵C、C′为对应点，点 A 为旋转中心，
∴AC＝AC′，
∴△ACC′为等腰三角形，
∴∠ACC′＝∠AC′C，
∵∠BAB′＝∠CAC′，∠AEB＝∠B′EP，∠B＝∠B′，
∴∠BAB′＝∠BPB′＝25°，
∴∠CAC′＝25°，
∴∠ACC′＝77.5°，
∴∠CAB＝77.5°，
故答案为：77.5°．
练习册系列答案
相关题目
