题目内容
四边形ABCD内接于圆,且CD=1,AB=
,BC=2,∠ABC=45°,则四边形ABCD的面积是( )
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
分析:根据AB=
,BC=2,∠ABC=45°可以推出BC是圆的直径.
过A作AF⊥BC于F,可以得到AF=BF=1,∠BAF=∠CAF=45°.
在直角三角形BCD中,由CD=1,BC=2可以得到∠DBC=30°,∠BCD=60°.
过D作DE⊥BC于E,可以求出DE=
;过D作DH⊥AF于H,接着求出AH,DH,然后就可以求出三角形AHD的面积,三角形ABF的面积,矩形DHFE的面积,三角形EDC的面积,最后即可求出四边形ABCD的面积.
| 2 |
过A作AF⊥BC于F,可以得到AF=BF=1,∠BAF=∠CAF=45°.
在直角三角形BCD中,由CD=1,BC=2可以得到∠DBC=30°,∠BCD=60°.
过D作DE⊥BC于E,可以求出DE=
| 3 |
解答: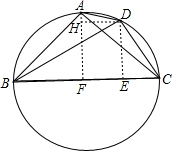 解:如图,过A作AF⊥BC于F.
解:如图,过A作AF⊥BC于F.
∵AB=
,∠ABC=45°,
∴BF=AF=1,
而BC=2,
∴F为CB中点,
∴AC=
,∠BAC=90°,
∴BC应该是圆的直径,
∴∠BAF=∠CAF=45°,
∴∠BDC=90°.
∴直角三角形BCD中,CD=1,BC=2,
∴∠DBC=30°,∠BCD=60°.
过D作DE⊥BC于E.
∴DE=
,
过D作DH⊥AF于H,
∴AH=
.
DH=CF-CE=1-1.5=0.5,
∴S△AHD=
.
而S△ABF=
,S矩形DHFE=
,S△EDC=
,
∴S四边形ABCD=S△ABF+S△AHD+S△DEC+S矩形DHFE=
.
故选D.
 解:如图,过A作AF⊥BC于F.
解:如图,过A作AF⊥BC于F.∵AB=
| 2 |
∴BF=AF=1,
而BC=2,
∴F为CB中点,
∴AC=
| 2 |
∴BC应该是圆的直径,
∴∠BAF=∠CAF=45°,
∴∠BDC=90°.
∴直角三角形BCD中,CD=1,BC=2,
∴∠DBC=30°,∠BCD=60°.
过D作DE⊥BC于E.
∴DE=
| 3 |
过D作DH⊥AF于H,
∴AH=
4-
| ||
| 2 |
DH=CF-CE=1-1.5=0.5,
∴S△AHD=
2-
| ||
| 8 |
而S△ABF=
| 1 |
| 2 |
| ||
| 4 |
| ||
| 8 |
∴S四边形ABCD=S△ABF+S△AHD+S△DEC+S矩形DHFE=
3+
| ||
| 4 |
故选D.
点评:此题首先通过作辅助线把一般四边形的面积问题转换为几个规则图形的面积的和差,此题关键是根据边的长和角的度数来得出特殊三角形从而求出四边形的面积.

练习册系列答案
相关题目
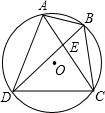 如图,已知四边形ABCD内接于⊙O,对角线AC,BD交于点E,求证:
如图,已知四边形ABCD内接于⊙O,对角线AC,BD交于点E,求证: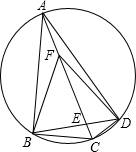 求证:
求证: (1997•海淀区)如图,四边形ABCD内接于半圆O,AB为直径,过点D的切线交BC的延长线于点E.若BE⊥DE,AD+DC=40,⊙O的半径为
(1997•海淀区)如图,四边形ABCD内接于半圆O,AB为直径,过点D的切线交BC的延长线于点E.若BE⊥DE,AD+DC=40,⊙O的半径为 如图,四边形ABCD内接于⊙O,若∠BOD=140°,则它的一个外角∠DCE=
如图,四边形ABCD内接于⊙O,若∠BOD=140°,则它的一个外角∠DCE=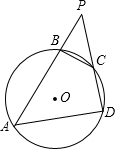 已知四边形ABCD内接于⊙O,分别延长AB和DC相交于点P,
已知四边形ABCD内接于⊙O,分别延长AB和DC相交于点P,