题目内容
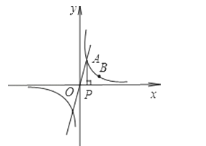
【题目】已知正比例函数y=2x的图象与反比例函数y=![]() (k≠0)在第一象限的图象交于A点,过A点作x轴的垂线,垂足为P点,已知△OAP的面积为1.
(k≠0)在第一象限的图象交于A点,过A点作x轴的垂线,垂足为P点,已知△OAP的面积为1.
(1)求反比例函数的解析式;
(2)如果点B为反比例函数在第一象限图象上的点(点B与点A不重合),且点B的横坐标为2,在x轴上求一点M,使MA+MB最小.
【答案】(1)y=![]() .(2)M点的坐标为(
.(2)M点的坐标为(![]() ,0).
,0).
【解析】
试题(1)设出A点的坐标,根据△OAP的面积为1,求出xy的值,得到反比例函数的解析式;
(2)作点A关于x轴的对称点A′,连接A′B,交x轴于点M,得到MA+MB最小时,点M的位置,求出直线A′B的解析式,得到它与x轴的交点,即点M的坐标.
试题解析:(1)设A点的坐标为(x,y),则OP=x,PA=y,
∵△OAP的面积为1,∴![]() xy=1,xy=2,即k=2,
xy=1,xy=2,即k=2,
∴反比例函数的解析式为:y=![]() .
.
(2)作点A关于x轴的对称点A′,连接A′B,交x轴于点M,MA+MB最小,
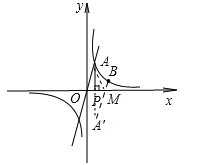
点B的横坐标为2,点B的纵坐标为y=![]() ="1,"
="1,"
两个函数图象在第一象限的图象交于A点,
2x=![]() ,x±1,y="±2,"
,x±1,y="±2,"
A点的坐标(1,2),
A关于x轴的对称点A′(1,-2),
设直线A′B的解析式为y="kx+b,"
![]()
解得![]()
直线y=3x-5与x轴的交点为(![]() ,0),
,0),
则M点的坐标为(![]() ,0).
,0).

练习册系列答案
相关题目
【题目】甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:

根据以上信息,整理分析数据如下:
平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
甲 | a | 7 | 7 | 1.2 |
乙 | 7 | b | 8 | c |
(1)写出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员.