Question

【题目】在平面直角坐标系xOy中，定义点P（x，y）的变换点为P′（x+y，x﹣y）．

（1）如图1，如果⊙O的半径为，

①请你判断M（2，0），N（﹣2，﹣1）两个点的变换点与⊙O的位置关系；

②若点P在直线y=x+2上，点P的变换点P′在⊙O的内，求点P横坐标的取值范围．

（2）如图2，如果⊙O的半径为1，且P的变换点P′在直线y=﹣2x+6上，求点P与⊙O上任意一点距离的最小值．

Answer 1

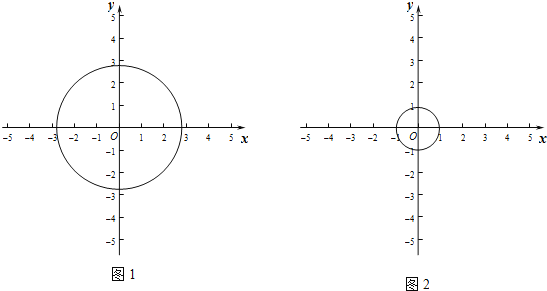
【答案】（1）①点N（﹣2，﹣1）的变换点在⊙O外；②点P横坐标的取值范围为﹣2＜x＜0；（2）点P与⊙O上任意一点距离的最小值为﹣1．

【解析】

试题分析：（1）①根据新定义得到点M的变换点M′的坐标为（2，2），于是根据勾股定理计算出OM′=2，则根据点与圆的位置关系的判定方法可判断点M的变换点在⊙O上；同样方法可判断点N（﹣2，﹣1）的变换点在⊙O外

②利用一次函数图象上点的坐标特征，设P点坐标为（x，x+2），利用新定义得到P点的变换点为P′的坐标为（2x+2，﹣2），则根据勾股定理计算出OP′=，然后利用点与圆的位置关系得到＜2，解不等式得﹣2＜x＜0；

（2）设点P′的坐标为（x，﹣2x+6），P（m，n），根据新定义得到m+n=x，m﹣n=﹣2x+6，消去x得3m+n=6，则n=﹣3m+6，于是得到P点坐标为（m，﹣3m+6），则可判断点P在直线y=﹣3x+6上，设直线y=﹣3x+6与x轴相交于点A，与y轴相交于点B，过O点作OH⊥AB于H，交⊙O于C，如图2，易得A（2，0），B（0，6），利用勾股定理计算出AB=2，再利用面积法计算出OH=，所以CH=﹣1，当点P在H点时，PC为点P与⊙O上任意一点距离的最小值．

解：（1）①M（2，0）的变换点M′的坐标为（2，2），则OM′==2，所以点M（2，0）的变换点在⊙O上；

N（﹣2，﹣1）的变换点N′的坐标为（﹣3，﹣1），则ON′==＞2，所以点N（﹣2，﹣1）的变换点在⊙O外；

②设P点坐标为（x，x+2），则P点的变换点为P′的坐标为（2x+2，﹣2），则OP′=，

∵点P′在⊙O的内，

∴＜2，

∴（2x+2）2＜4，即（x+1）2＜1，

∴﹣1＜x+1＜1，解得﹣2＜x＜0，

即点P横坐标的取值范围为﹣2＜x＜0；

（2）设点P′的坐标为（x，﹣2x+6），P（m，n），

根据题意得m+n=x，m﹣n=﹣2x+6，

∴3m+n=6，

即n=﹣3m+6，

∴P点坐标为（m，﹣3m+6），

∴点P在直线y=﹣3x+6上，

设直线y=﹣3x+6与x轴相交于点A，与y轴相交于点B，过O点作OH⊥AB于H，交⊙O于C，如图2，

则A（2，0），B（0，6），

∴AB==2，

∵OHAB=OAOB，

∴OH==，

∴CH=﹣1，

即点P与⊙O上任意一点距离的最小值为﹣1．