题目内容
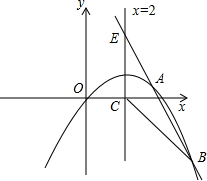
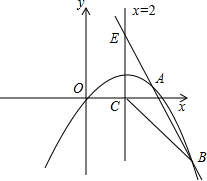 如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2 与x轴交于点C,直线y=-2x+7经过抛物线上一点B(5,m),且与直线x=2交于点E.
如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2 与x轴交于点C,直线y=-2x+7经过抛物线上一点B(5,m),且与直线x=2交于点E.
(1)求m的值及该抛物线的函数关系式;
(2)若点D是x轴上一动点,当△DCB∽△ECB时,求点D的坐标;
(3)若P(x,y)是该抛物线上的一个动点,是否存在这样的点P,使得PB=PC?若存在,试求出所有符合条件的点P的坐标;若不存在,请说明理由.
解:(1)∵点B(5,m)在直线y=-2x+7上,
∴m=-5×2+7=-3,
∴B(5,-3),
∵抛物线经过原点O和点A,对称轴为x=2,
∴点A的坐标为(4,0)
设所求的抛物线对应函数关系式为y=a(x-0)(x-4),
将点B(5,-3)代入上式,
得-3=a(5-0)(5-4),
∴a=- ,
,
∴所求的抛物线对应的函数关系式为y=- x(x-4),
x(x-4),
即y=- x2+
x2+ x.
x.
(2)∵点A(4,0),B(5,-3),C(2,0),
∴AC=4-2=2,BC= =3
=3 ,
,
当点D在直线x=2的右侧时,
当△DCB∽△ECB,
∴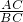 =
=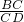 ,
,
即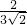 =
= ,
,
解得:CD=9,
∴点D的坐标为:(11,0),
当点D在直线x=2的左侧时,∵∠ACB=∠CDB+∠CBA,
且∠ACB<∠DCB,
∴在△DCB中不可能存在与∠DCB相等的角,
即此时不存在点使三角形相似;
综上所述,存在点D的坐标是(11,0),使三角形相似;
(3)存在符合条件的点P使PB=PC,
∵C(2,0),B(5,-3),
∴∠ACB=45°,
BC垂直平分线的解析式为:y=x-5,
∴ ,
,
∴解得: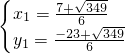 ,
,
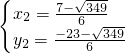 ,
,
∴符合条件的点P的坐标为( ,
, )或(
)或(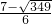 ,
,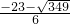 ).
).
分析:(1)根据抛物线的对称轴为x=2,且过O、A两点,因此A点的坐标为(4,0).可用交点式二次函数通式来设抛物线的解析式,然后根据直线y=-2x+7求出B点的坐标,将B点的坐标代入抛物线中即可求出二次函数的解析式.
(2)可根据点A(4,0),B(5,-3),C(2,0)坐标,当点D在直线x=2的右侧时,进而得出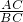 =
=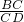 ,进而得出CD的长.当点D在直线x=2的左侧时,得出在△DCB中不可能存在与∠DCB相等的角,进而得出答案.
,进而得出CD的长.当点D在直线x=2的左侧时,得出在△DCB中不可能存在与∠DCB相等的角,进而得出答案.
(3)由题意可知:P点必为线段BC垂直平分线与抛物线的交点,可先求出线段BC的垂直平分线,然后联立抛物线的解析式,即可求出符合条件的P点的坐标.
点评:此题主要考查了待定系数法求以一次函数解析式以及顶点式求二次函数解析式以及函数交点坐标求法等知识,结合数形结合熟练应用函数交点求法是解决问题的关键.
∴m=-5×2+7=-3,
∴B(5,-3),
∵抛物线经过原点O和点A,对称轴为x=2,
∴点A的坐标为(4,0)
设所求的抛物线对应函数关系式为y=a(x-0)(x-4),
将点B(5,-3)代入上式,
得-3=a(5-0)(5-4),
∴a=-
 ,
,
∴所求的抛物线对应的函数关系式为y=-
 x(x-4),
x(x-4),即y=-
 x2+
x2+ x.
x.(2)∵点A(4,0),B(5,-3),C(2,0),
∴AC=4-2=2,BC=
 =3
=3 ,
,当点D在直线x=2的右侧时,
当△DCB∽△ECB,
∴
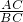 =
=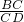 ,
,即
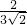 =
= ,
,解得:CD=9,
∴点D的坐标为:(11,0),
当点D在直线x=2的左侧时,∵∠ACB=∠CDB+∠CBA,
且∠ACB<∠DCB,
∴在△DCB中不可能存在与∠DCB相等的角,
即此时不存在点使三角形相似;
综上所述,存在点D的坐标是(11,0),使三角形相似;
(3)存在符合条件的点P使PB=PC,
∵C(2,0),B(5,-3),
∴∠ACB=45°,
BC垂直平分线的解析式为:y=x-5,
∴
 ,
,∴解得:
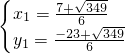 ,
,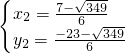 ,
,∴符合条件的点P的坐标为(
 ,
, )或(
)或(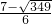 ,
,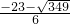 ).
).分析:(1)根据抛物线的对称轴为x=2,且过O、A两点,因此A点的坐标为(4,0).可用交点式二次函数通式来设抛物线的解析式,然后根据直线y=-2x+7求出B点的坐标,将B点的坐标代入抛物线中即可求出二次函数的解析式.
(2)可根据点A(4,0),B(5,-3),C(2,0)坐标,当点D在直线x=2的右侧时,进而得出
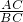 =
=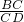 ,进而得出CD的长.当点D在直线x=2的左侧时,得出在△DCB中不可能存在与∠DCB相等的角,进而得出答案.
,进而得出CD的长.当点D在直线x=2的左侧时,得出在△DCB中不可能存在与∠DCB相等的角,进而得出答案.(3)由题意可知:P点必为线段BC垂直平分线与抛物线的交点,可先求出线段BC的垂直平分线,然后联立抛物线的解析式,即可求出符合条件的P点的坐标.
点评:此题主要考查了待定系数法求以一次函数解析式以及顶点式求二次函数解析式以及函数交点坐标求法等知识,结合数形结合熟练应用函数交点求法是解决问题的关键.

练习册系列答案
相关题目
 2x+1经过抛物线上一点B(2,m),且与y轴.直线x=-2分别交于点D、E.
2x+1经过抛物线上一点B(2,m),且与y轴.直线x=-2分别交于点D、E. (2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1.
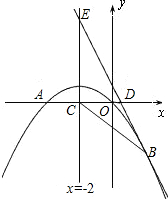
(2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1.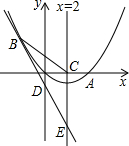 如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E,
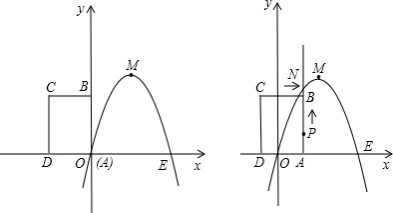
如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E,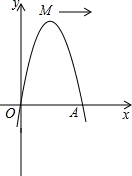 如图,已知抛物线经过坐标原点,与x轴的另一个交点为A,且顶点M坐标为(1,2),
如图,已知抛物线经过坐标原点,与x轴的另一个交点为A,且顶点M坐标为(1,2),