题目内容
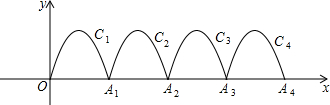
(2013•葫芦岛)如图,一段抛物线C1:y=-x(x-3)(0≤x≤3)与x轴交于点O,A1;将C1向右平移得第2段抛物线C2,交x轴于点A1,A2;再将C2向右平移得第3段抛物线C3,交x轴于点A2,A3;又将C3向右平移得第4段抛物线C4,交x轴于点A3,A4,若P(11,m)在C4上,则m的值是
2
2
.
分析:利用抛物线C1的解析式求出A1的坐标为(3,0),然后确定出平移到C4的平移距离,并求出平移后的顶点坐标,然后写出顶点式解析式,最后把点P的坐标代入进行计算即可得解.
解答:解:令y=0,则-x(x-3)=0,
解得x1=0,x2=3,
∴点A1(3,0),
由题意得,平移到C4的平移距离为3×3=9,
∵y=-x(x-3)=-(x-
)2+
,
∴C4的解析式为:y=-(x-
-9)2+
,
∵P(11,m)在C4上,
∴m=-(11-
-9)2+
=-
+
=2.
故答案为:2.
解得x1=0,x2=3,
∴点A1(3,0),
由题意得,平移到C4的平移距离为3×3=9,
∵y=-x(x-3)=-(x-
| 3 |
| 2 |
| 9 |
| 4 |
∴C4的解析式为:y=-(x-
| 3 |
| 2 |
| 9 |
| 4 |
∵P(11,m)在C4上,
∴m=-(11-
| 3 |
| 2 |
| 9 |
| 4 |
| 1 |
| 4 |
| 9 |
| 4 |
故答案为:2.
点评:本题考查了二次函数图象与几何变换,求出平移的距离并利用写出C4的顶点式解析式是解题的关键,也是本题的难点.

练习册系列答案
相关题目
 (2013•葫芦岛)如图,AB是半圆的直径,AB=2,∠B=30°,则
(2013•葫芦岛)如图,AB是半圆的直径,AB=2,∠B=30°,则
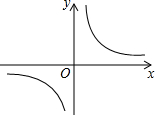 (2013•葫芦岛)如图是反比例函数y=
(2013•葫芦岛)如图是反比例函数y=