题目内容
【题目】如图,在△ABC中,分别延长△ABC的边AB,AC到D,E,∠CBD与∠BCE的平分线相交于点P,爱动脑筋的小明在写作业时发现如下规律: a.若∠A=50°,则∠P=65°=90°﹣ ![]() ;
;
b.若∠A=90°,则∠P=45°=90°﹣ ![]() ;
;
c.若∠A=100°,则∠P=40°=90°﹣ ![]() ;
;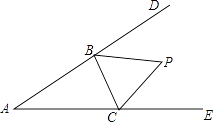
(1)根据上述规律,若∠A=150°,则∠P=;
(2)请你用数学表达式归纳出∠P与∠A的关系;
(3)请说明你的结论.
【答案】
(1)解:15°
(2)解:∠P与∠A的关系为∠P=90°﹣ ![]() ∠A
∠A
(3)解:理由如下:
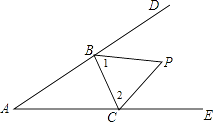
如图,
∵∠CBD与∠BCE的平分线相交于点P,
∴∠1= ![]() ∠DBC,∠2=
∠DBC,∠2= ![]() ∠BCE,
∠BCE,
∵∠P=180°﹣∠1﹣∠2=180°﹣ ![]() (∠DBC+∠BCE),
(∠DBC+∠BCE),
而∠DBC=180°﹣∠ABC,∠BCE=180°﹣∠ACB,
∴∠P=180°﹣ ![]() (180°﹣∠ABC+180°﹣∠ACB)
(180°﹣∠ABC+180°﹣∠ACB)
= ![]() (∠ABC+∠ACB),
(∠ABC+∠ACB),
而∠ABC+∠ACB=180°﹣∠A,
∴∠P= ![]() (180°﹣∠A)=90°﹣
(180°﹣∠A)=90°﹣ ![]() ∠A.
∠A.
【解析】解:(1)若∠A=150°,则∠P=90°﹣ ![]() =15°;所以答案是15°;
=15°;所以答案是15°;
【考点精析】利用三角形的内角和外角对题目进行判断即可得到答案,需要熟知三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.

练习册系列答案
相关题目