Question

抛物线y=ax²+2ax+b与直线y=x+1交于A、C两点，与y轴交于B，AB∥x轴，且S_△ABC=3，A点坐标为（-2，b）．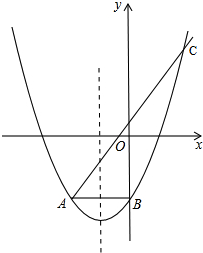

（1）求抛物线的解析式；
（2）P为x轴负半轴上一点，以AP、AC为边作平行四边形CAPQ，是否存在P，使得Q点恰好在此抛物线上？若存在，请求出P、Q的坐标；若不存在，请说明理由；
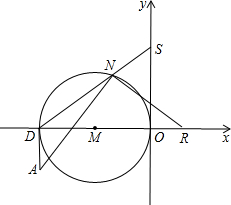
（3）AD⊥x轴于D，以OD为直径作⊙M，N为⊙M上一动点，（不与O、D重合），过N作AN的垂线交x轴于R点，DN交y轴于点S，当N点运动时，线段OR、OS是否存在确定的数量关系写出证明．

Answer 1

分析：（1）先根据直线AC的解析式求出A、C的坐标，然后代入抛物线中即可求得二次函数的解析式．
（2）可设出P点坐标，根据已知的平行四边形的三点坐标表示出Q点坐标，已知了Q点在抛物线上，将Q点坐标代入抛物线的解析式中即可求出Q点坐标．
（3）本题可根据相似三角形求解．连接ON后可得出∠RNO和∠AND同为∠ANO的余角，因此两角相等，而∠ADN与∠NOR都是90°加上一个等角（根据弦切角定理可得）．因此△AND∽△RON，可得出关于OR、AD、ON、AN的比例关系式．同理可在相似三角形DON和OSN中得出关于OS、OD、ON、AN的比例关系式，将等值替换后可得出OR：OS=AD：OD，即A点纵坐标绝对值与横坐标绝对值的比为1：2．

解答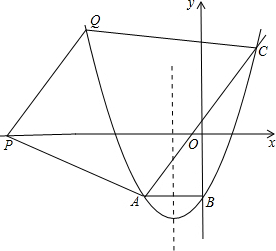：解：（1）抛物线对称轴为直线x=-

2a

2a

=-1，则AB=2，将A（-2，b）代入y=x+1中，得b=-1，
联立

y=ax2+2ax-1 y=x+1

，得

x=-2 y=-1

或

x= 1 a y= 1 a +1

，由AB=2，S_△ABC=3，
可知（

1

a

+1）-（-1）=3，解得a=1，
∴y=x²+2x-1．

（2）联立

y=x2+2x-1 y=x+1

，
得A（-2，-1）C（1，2），
设P（a，0），则Q（3+a，3）
∴（3+a）²+2（3+a）-1=3，
∴a₁=-4-

5

，a₂=-4+

5

，
∴P（-4-

5

，0）或（-4+

5

，0）
∴Q（-1-

5

，3）或（-1+

5

，3）．

（3）∵△AND∽△RON，
∴

OR

AD

=

ON

DN

，
又∵△ONS∽△DNO，
∴

OS

OD

=

ON

DN

=

1

2

，
∴

OR

OS

=

1

2

．

点评：本题主要考查了二次函数和圆的相关知识，综合性强，难度较大．