题目内容
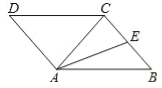
【题目】在矩形ABCD中,AB=1,AD=![]() ,AF平分∠DAB,过C点作CE⊥BD于E,延长AF.EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED.正确的是( )
,AF平分∠DAB,过C点作CE⊥BD于E,延长AF.EC交于点H,下列结论中:①AF=FH;②BO=BF;③CA=CH;④BE=3ED.正确的是( )

A. ②③ B. ③④ C. ①②④ D. ②③④
【答案】D
【解析】∵矩形ABCD,
∴AD∥BC,![]() ,AO=OC,OD=OB,AC=BD,
,AO=OC,OD=OB,AC=BD,
∴AO=OB=OD,
∵AB=1,AD=![]() ,由勾股定理得:AC=2,
,由勾股定理得:AC=2,
∴∠ABD=60°,
∴△ABO是等边三角形,
∴AB=OA=OB, ∠BAO=∠AOB=60°,
∵AF平分∠BAD,
∴∠BAF=∠DAF=45°,
∵∠DAF=∠AFB,
∴∠BAF=∠BFA,![]() ,∴②正确;
,∴②正确;
∵CE⊥BD,![]() ,
,
∴∠ECO=30°,![]() ,
,![]() ,
,
∴AC=CH, ∴③正确;
∵CF和AH不垂直, ∴AF≠FH, ∴①错误;
∵∠CEO=90°, ∠ECA=30°,![]() ,
,
BE=3DE, ∴④正确.
正确的有②③④,故选D.
点睛;本题主要考查对等腰三角形的性质,勾股定理,三角形的外角性质,矩形的性质,平行线的性质,等边三角形的性质和判定等知识点的理解和掌握,综合运用这些性质进行推理是解此题的关键.

练习册系列答案
相关题目
【题目】如图1表示同一时刻的韩国首尔时间和北京时间,两地时差为整数.
(1)设北京时间为x(时),首尔时间为y(时),就0≤x≤12,求y关于x的函数表达式,并填写下表(同一时刻的两地时间).
北京时间 | 7:30 | 11:15 | 2:50 |
首尔时间 | 8:30 | 12:15 | 3:50 |
(2)如图2表示同一时刻的英国伦敦时间(夏时制)和北京时间,两地时差为整数.如果现在伦敦(夏时制)时间为7:30,那么此时韩国首尔时间是多少?