题目内容
已知关于x的一元二次方程x2-2mx+m2-2m=0。
(1)当m=1时,求方程的根;
(2)试判断此方程根的情况;
(3)若x1、x2是方程的两个实数根,满足x2>x1且x2<x1+3;当m是整数时,求m的值。
(1)当m=1时,求方程的根;
(2)试判断此方程根的情况;
(3)若x1、x2是方程的两个实数根,满足x2>x1且x2<x1+3;当m是整数时,求m的值。
解:(1)当m=1时,原方程为x2-2x-1=0,
解得 x=1±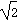 ;
;
(2)△=8m,
①当m>0时,原方程有两不等实根;
②当m=0时,原方程有两相等实根;
③当m<0时,原方程无实根;
(3)由已知,可得:0<x2-x1<3 两边平方可得到:
(x1+ x2)2-4 x1x2<9
即8m<9,
解得m<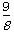
而x1≠ x2且m为整数
∴m=1。
解得 x=1±
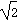 ;
;(2)△=8m,
①当m>0时,原方程有两不等实根;
②当m=0时,原方程有两相等实根;
③当m<0时,原方程无实根;
(3)由已知,可得:0<x2-x1<3 两边平方可得到:
(x1+ x2)2-4 x1x2<9
即8m<9,
解得m<
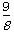
而x1≠ x2且m为整数
∴m=1。

练习册系列答案
相关题目
已知关于x的一元二次x2-6x+k+1=0的两个实数根x1,x2,
+
=1,则k的值是( )
| 1 |
| x1 |
| 1 |
| x2 |
| A、8 | B、-7 | C、6 | D、5 |
 .
. .
.