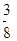题目内容
(本小题满分8分)
如图所示,小吴和小黄在玩转盘游戏,准备了两个可以自由转动的转盘甲、乙,每个转盘被分成面积相等的几个扇形区域,并在每个扇形区域内标上数字,游戏规则:同时转动两个转盘,当转盘停止转动后,指针所指扇形区域内的数字之和为4,5或6时,则小吴胜;否则小黄胜。(如果指针恰好指在分割线上,那么重转一次,直到指针指向某一扇形区域为止)

(1)这个游戏规则对双方公平吗?说说你的理由;
(2)请你设计一个对双方都公平的游戏规则。
如图所示,小吴和小黄在玩转盘游戏,准备了两个可以自由转动的转盘甲、乙,每个转盘被分成面积相等的几个扇形区域,并在每个扇形区域内标上数字,游戏规则:同时转动两个转盘,当转盘停止转动后,指针所指扇形区域内的数字之和为4,5或6时,则小吴胜;否则小黄胜。(如果指针恰好指在分割线上,那么重转一次,直到指针指向某一扇形区域为止)

(1)这个游戏规则对双方公平吗?说说你的理由;
(2)请你设计一个对双方都公平的游戏规则。
(1)不公平
(2)

解:列表或画树状图正确,

(1)数字之和一共有20种情况,和为4,5或6的共有11种情况,
∵P(小吴胜)= >P(小黄胜)=
>P(小黄胜)= ,
,
∴这个游戏不公平;
(2)新的游戏规则:和为奇数小吴胜,和为偶数小黄胜.
理由:数字和一共有20种情况,和为偶数、奇数的各10种情况,
∴P(小吴胜)=P(小黄胜)= .
.
| 转盘甲 转盘乙 | 1 | 2 | 3 | 4 | 5 |
| 1 | (1,1)和为2 | (2,1)和为3 | (3,1)和为4 | (4,1)和为5 | (5,1)和为6 |
| 2 | (1,2)和为3 | (2,2)和为4 | (3,2)和为5 | (4,2)和为6 | (5,2)和为7 |
| 3 | (1,3)和为4 | (2,3)和为5 | (3,3)和为6 | (4,3)和为7 | (5,3)和为8 |
| 4 | (1,4)和为5 | (2,4)和为6 | (3,4)和为7 | (4,4)和为8 | (5,4)和为9 |

(1)数字之和一共有20种情况,和为4,5或6的共有11种情况,
∵P(小吴胜)=
 >P(小黄胜)=
>P(小黄胜)= ,
,∴这个游戏不公平;
(2)新的游戏规则:和为奇数小吴胜,和为偶数小黄胜.
理由:数字和一共有20种情况,和为偶数、奇数的各10种情况,
∴P(小吴胜)=P(小黄胜)=
 .
.
练习册系列答案
相关题目





 ;
;  ”表示抽奖l00次就一定会中奖;
”表示抽奖l00次就一定会中奖; .
.