题目内容
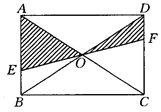
如图，在平行四边形ABCD中，E、F分别在AB、CD边上，且AE＝CF。
（1）求证：△ADE≌△CBF；
（2）求证：四边形BFDE是平行四边形。
（1）求证：△ADE≌△CBF；
（2）求证：四边形BFDE是平行四边形。
（1）证明见解析；（2）证明见解析.
试题分析：（1）利用平行四边形ABCD的对角相等，对边相等的性质推知∠A=∠C，AD=BC；然后根据全等三角形的判定定理AAS证得结论；
（2）由“对边平行且相等的四边形是平行四边形”推知四边形DEBF是平行四边形．
试题解析：（1）证明：∵四边形ABCD为平行四边形，
∴∠A=∠C，AD=BC，
在△ADE与△CBF中，
，∴△ADE≌△CBF（ASA）；
（2）解：四边形DEBF是平行四边形．理由如下：
∵DF∥EB，又由△ADE≌△CBF，知AE=CF，
∴AB-AE=CD-CF，即DF=EB．
∴四边形DEBF是平行四边形．
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
相关题目
外侧作直线
，点
关于直线
，连接
，其中
交直线
．
，求
的度数；
，用等式表示线段
之间的数量关系，并证明．
. 在旋转过程中，两个正方形只有点A重合，其它顶点均不重合，连接BE、DG.
，求点G到BE的距离.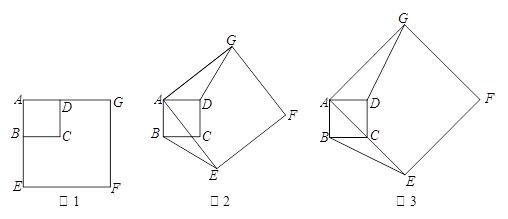
．
=
，则△CEF≌△CDF．
ABCD中，∠ABC的平分线交AD于E，∠BED=150°，则∠A的大小为（ ）
