题目内容
如图,已知网格中每个正方形的边长都是1,图中的阴影图案是由两段以格点为圆心,分别以小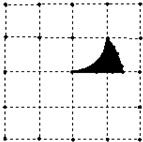 正方形的边长和对角线长为半径的圆弧和网格的边围成.
正方形的边长和对角线长为半径的圆弧和网格的边围成.(1)计算图中阴影部分的面积;
(2)请你在网格中以阴影图案为基本图案,借助轴对称、平移或旋转设计一个完整的图案(要求至少含有两种图形变换).
分析:(1)从图中可以发现阴影部分的面积等于以对角线为半径的扇形面积减弓形面积,根据面积公式计算即可.
(2)作一个轴对称图形和一个顺时针旋转90度的图形,组成一个花.
(2)作一个轴对称图形和一个顺时针旋转90度的图形,组成一个花.
解答: 解:(1)根据勾股定理得:
解:(1)根据勾股定理得:
对角线长=
所以以对角线为半径所组成的扇形面积=
=
以正方形的边长为半径的扇形面积=
=
则图中的弓形面积=
-
则阴影部分的面积=
-(
-
)=
.
(2)作图如右图.
 解:(1)根据勾股定理得:
解:(1)根据勾股定理得:对角线长=
| 2 |
所以以对角线为半径所组成的扇形面积=
| 45π×2 |
| 360 |
| π |
| 4 |
以正方形的边长为半径的扇形面积=
| 90π×1 |
| 360 |
| π |
| 4 |
则图中的弓形面积=
| π |
| 4 |
| 1 |
| 2 |
则阴影部分的面积=
| π |
| 4 |
| π |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)作图如右图.
点评:本题综合考查了扇形,三角形及勾股定理和图形变换的知识.学生对学过的知识要会灵活运用.

练习册系列答案
相关题目
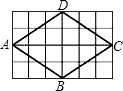 如图,已知网格中每个小正方形的边长为1,则菱形ABCD的面积为
如图,已知网格中每个小正方形的边长为1,则菱形ABCD的面积为 如图.已知网格中每个小正方形的边长都是1,图1中的四边形ABCD的对边互相平行(即AB∥DC,AD∥BC),∠BAC=∠BCA=m°.
如图.已知网格中每个小正方形的边长都是1,图1中的四边形ABCD的对边互相平行(即AB∥DC,AD∥BC),∠BAC=∠BCA=m°. 正方形的边长和对角线长为半径的圆弧和网格的边围成.
正方形的边长和对角线长为半径的圆弧和网格的边围成.
